UFRJ – Física 1 – Segunda Chamada – 2022.1
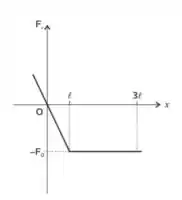
3) Uma partícula se move ao longo do eixo sob a ação de uma força total dependente apenas da posição e cujo gráfico está ilustrado na figura. Em , a partícula está na origem e tem velocidade . Ao atingir a posição , ela tem velocidade nula. Nessas condições, ao obtermos o módulo da velocidade da partícula na origem em termos de e encontraremos:
a)
b)
c)
d)
e)
Passo 1
Fala aí, galerinha!! Nessa questão a gente tem uma partícula que anda em linha reta sob a ação de uma força que varia ao longo da posição da partícula de acordo com esse gráfico aqui:
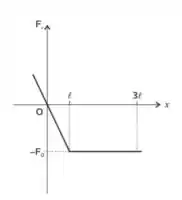
O enunciado nos fala que a partícula sai da origem com velocidade e aí ele nos pede para encontrar esse valor sabendo que no fim do trajeto, , a velocidade da partícula é nula.
Esse é um exercício em que a gente vai ter que usar o teorema trabalho-energia cinética:
Só que o trabalho a gente consegue calcular através do gráfico:
Então vamos usar essas informações para obter aquele !Partiiiiiu
Passo 2
Vamos começar calculando o trabalho realizado pela força no deslocamento de até . Para isso vamos ter que calcular a área desse trapézio que a gente tem né?É importante lembrar que como o gráfico está abaixo do eixo , o trabalha vai ser negativo. Então a gente calcula a área normalmente e acrescenta um sinal de menos no final:
Onde é a área do trapézio de base maior , base menor e altura . A área do trapézio é calculada através de:
Então o trabalho realizado pela força nesse deslocamento é:
Passo 3
Agora que a gente já tem o trabalho total realizado pela força, vamos usar o teorema trabalho-energia cinética para encontrar :
O enunciado nos diz que ao fim do deslocamento a velocidade da partícula é nula, então temos . A expressão fica:
Usando o valor do trabalho que encontramos temos:
Isolando para :E aí resolvemos essa 😊 Vamos para a próxima??