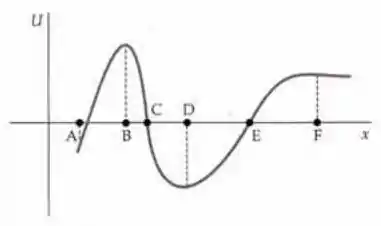
A figura mostra o gráfico de uma função energia potencial .
- Para cada ponto indicado, informa se a componente x da força associada a esta função é positiva, negativa ou zero.
- Em que ponto a força tem a maior magnitude?
Passo 1
Alternativa a)
Já começo falando pra tu ter atenção ali no ponto A pra ver onde ele ta direitinho, porque ele não está em cima do eixo x!
Agora voltando pra analisar, vamos usar essa paradinha aqui ó
Como o gráfico é justamente o gráfico do potencial, vamos analisar só a derivada, se a derivada for positiva a força é negativa, se a derivada for negativa a força é positiva.
Passo 2
Como a derivada no ponto é positiva, a força é negativa!
Como a derivada no ponto é zero, a força é nula!
Como a derivada no ponto é negativa, a força é positiva!
Como a derivada no ponto é zero, a força é nula!
Como a derivada no ponto é positiva, a força é negativa!
Como a derivada no ponto é zero, a força é nula!
Quadro resuminho:
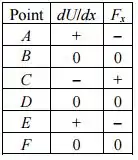
Passo 3
Alternativa b)
Agora temos que encontrar em que ponta a força tem maior magnitude. O que isso quer dizer?
Que temos que achar o ponto que apresenta a menor derivada! Se analisarmos no gráfico, esse será o ponto C.
Resposta
a)
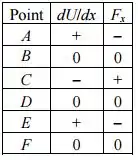
b) O ponto C.