Exercícios Resolvidos de Reta Tangente e Normal a Curva

Exercício 30 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58

Enunciado

Cálculo - James Stewart - Volume 2 - 7ª Edição – Capítulo 13 – Seção 2 – Exercício 4

(Capítulo 13.2 – Exercício 4)

(a) Esboce o gráfico da curva plana com a equação vetorial dada.

(b) Encontre r’(t)

(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.

Passo 1

Oieeee gente!!

Vamos lá, nesse exercício, temos uma curva , e aí queremos:

- Esboçar o gráfico dessa curva

- Encontrar a derivada da curva

- Esboçar o vetor da curva no valor dado de , junto com o vetor tangente

Vamosss que vai ser tranquilíssimo, blz?

Passo 2

Passo 3

a) Temos a curva:

Podemos escrever isso como equações paramétricas, assim:

Sabendo que , temos

Manipulando a expressão:

Então podemos escrever

Então essa é a nossa curva:

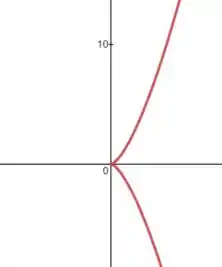
Passo 4

b) Agora queremos derivar a curva . A derivada do vetor r é dada pela derivada de cada componente individualmente:

Fechou?

Passo 5

c) O vetor posição em é

Por outro lado, o vetor tangente em , tem origem no ponto (1,1) e é dado por

Então, podemos representar esses vetores conforme mostrado na figura abaixo:

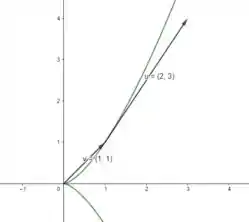
E fimmm

Resposta

a)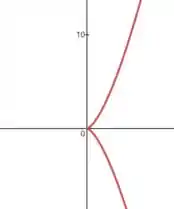

b)

c)

Exercícios de Livros Relacionados

Calcule a inclinação da reta tangente para a curva polar dada no ponto especificado pelo valor de θ . r = 1 + 2 c o s θ θ = π 3

Mostre que a equação da reta tangente à parábola y 2 = 4 p x no ponto x 0 , y 0 pode ser escrita como y 0 y = 2 p ( x + x 0 ) Onde essa reta tangente intercepta o eixo x ? Use esse fato para desenhar

Encontre d y / d x e d ² y / d x ² ² ². Para quais valores de t a curva é côncava para cima? x = t - ln ⁡ t y = t + ln ⁡ t

Nos exercícios 9 a 20, determine os pontos nos quais a curva dada tem retas tangentes verticais e horizontais. Faça um esboço do gráfico e mostre essas retas tangentes14. r = 3 - 3 c o s θ

a) Encontre a inclinação da reta tangente à trocoide x = r θ - ds e nθ , y = r - d cos ⁡ θ em termos de θ .b) Mostre que, se dr , então a trocoide não tem uma tangente vertical.