Livro James Stewart, Volume 2, 7ª Edição, Capítulo 13, Seção 2, Exercício 29
(Cap. 13.2 - Ex. 29)Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado. Ilustre traçando o gráfico da curva e da reta tangente em uma mesma tela.
Passo 1
Faala, pessoal! Tudo bem com vocês? Vamos lá resolver mais uma questão?
Esse exercício aqui é daqueles que tem o enunciado bem direto, então vamos ter que fazer poucas interpretações, o que vai ajudar bastante nossa vida!
O objetivo aqui é encontrar as equações paramétricas pra uma reta tangente à uma curva que foi dada. E o que isso quer dizer?
Precisamos lembrar aqui, que se a gente tem uma curva parametrizada (que vamos chamar de ), e temos um ponto nessa mesma curva, esse ponto nada mais é do que a seguinte junção: , que é chamada de equação vetorial.
Essa sacada do que compõe esse ponto em uma curva parametrizada vai ser a chave pra gente resolver esse probleminha aqui!
Então, seguindo a linha de raciocínio, se eu quero encontrar as equações paramétricas da reta tangente, nós vamos precisar de um ponto e uma direção. Se a gente tiver um ponto e uma direção, encontramos a reta. E pra esse caso aqui, a direção será dada pela derivada, já que queremos a reta tangente, e o ponto o enunciado deu pra gente.
Bom, então, primeiro vamos escrever a equação vetorial para a curva, a partir dos dados que foram fornecidos no enunciado:
E partindo pra derivada, nós vamos utilizar o método da derivada termo a termo:
Passo 2
Agora, a gente vai determinar o tempo para que a curva esteja no ponto . Para isso, vamos usar o ponto dado no enunciado, e a equação vetorial da curva.
O valor do parâmetro no ponto considerado é já que temos:
Com o valor de encontrado, vamos substituir ele nas derivadas de e feitas no item anterior. Isso vai dar pra gente o vetor tangente:
Com isso, a gente consegue ver aqui, que a linha tangente é paralela ao vetor e inclui o ponto .
Passo 3
Seguindo a questão, pra gente encontrar as equações paramétricas, da literatura, sabemos que a equação paramétrica é a soma do ponto com o vetor . Então:
Fazendo isso para e , vamos ter que:
Organizando melhor as equações acima, temos que:
Passo 4
Por fim, com base nas equações paramétricas da curva e da reta é possível traçar os gráficos de ambas numa mesma tela utilizando softwares. O gráfico para essa questãozinha aqui está mostrado abaixo:
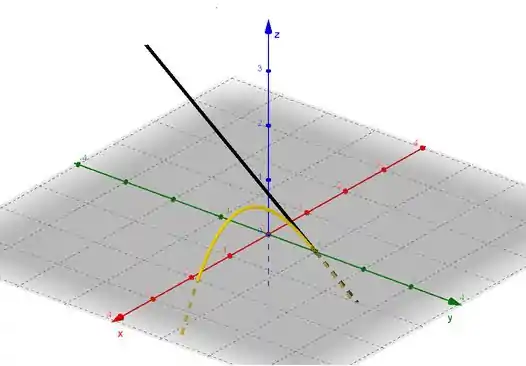
Pra essa questão é isso, pessoal!! Bora resolver mais uma??
Resposta
