Livro James Stewart, Volume 2, 7ª Edição, Capítulo 13, Seção 2, Exercício 32
(Cap. 13.2 - Ex. 32) (a) Determine o ponto de intersecção das retas tangentes à curva
nos pontos e .
(b) Ilustre traçando o gráfico da curva e ambas as tangentes.
Passo 1
Faaala, galerinha!! Vamos lá resolver essa questãozinha juntos?
O enunciado desse exercício aqui é bem direto e já passa pra gente algumas equações que serão importantes pra entender como vamos resolver. Então bora lá!
O objetivo aqui é determinar o ponto de intersecção das retas tangentes à curva, em dois pontos específicos. E o que significa isso? Nada mais é do que o ponto em que as retas tangentes vão se cruzar!
Ta, mas e agora? Como encontramos esse ponto?
Pra determinar o ponto onde retas tangentes se cruzam, a gente vai precisar encontrar a equação paramétrica de cada uma dessas retas. Pra isso, vamos precisar de um ponto, e um vetor que pertence a essa reta.
Bora começar encontrando essas equações então?
A primeira coisa a se fazer é obter o obter o vetor posição , dado no enunciado, nos pontos de tangência e , que foram os pontos que o exercício pediu pra gente.
Pra isso, basta substituir os valores do parâmetro na equação da curva:
Passo 2
O segundo passo é calcular a derivada de que representa a equação geral do vetor tangente a esse curva:
Logo, nos pontos de tangência e , os vetores tangentes serão dados por
Passo 3
Agora que sabemos os pontos e os vetores de tangência é possível calcular as equações das retas tangentes à curva nos pontos dados.
A reta tangente em é a reta que parte do vetor posição da curva e tem a direção do vetor tangente . Portanto, chamando essa reta de , temos:
Já a reta tangente em é a reta que parte do vetor posição da curva e tem a direção do vetor tangente . Portanto, chamando essa reta de w, temos:
As retas se interceptam quando , ou seja:
Logo, o ponto de intersecção da reta é .
Passo 4
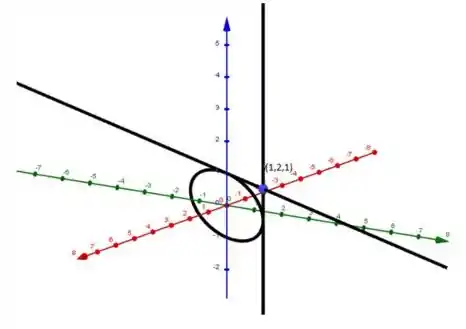
Por fim, vamos usar um software, onde colocaremos a equação da curva, juntamente com as equações das retas tangentes, e formar assim o gráfico pedido no item (b).
Pra essa questão é isso, pessoal!! Bora resolver mais uma??
Resposta
a) Ponto de intersecção:
b) Gráfico:
