Cálculo - James Stewart - Volume 2 - 7ª Edição – Capítulo 13 – Seção 1 – Exercício 14
(Capítulo 13.1 – Exercício 14) Esboce o gráfico da curva cuja equação vetorial é dada. Indique com setas a direção na qual o parâmetro t cresce.
Passo 1
E aíí pessoal, belezinha?
Vamos lá, nessa questão estamos falando sobre esboço de gráfico pra funções vetoriais
Queremos esboçar o gráfico da seguinte função paramétrica, mostrando a direção em que o parâmetro cresce:
Vamos lá?
Passo 2
As coordenadas e da equação paramétrica são, respectivamente:
Como e são iguais, porém com sinais opostos, podemos escrever
Além disso, como e , podemos escrever, pela relação fundamental trigonométrica:
Assim, temos um círculo no eixo cuja coordenada vai aumentando conforme o valor de .
Passo 3
Para verificarmos de que forma o parâmetro cresce, vamos observar alguns valores de :
Assim o parâmetro cresce seguindo o caminho:
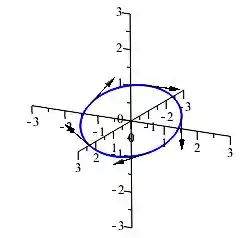
O gráfico da equação é:
Resposta
