Cálculo - James Stewart - Volume 2 - 7ª Edição – Capítulo 13 – Seção 1 – Exercício 21
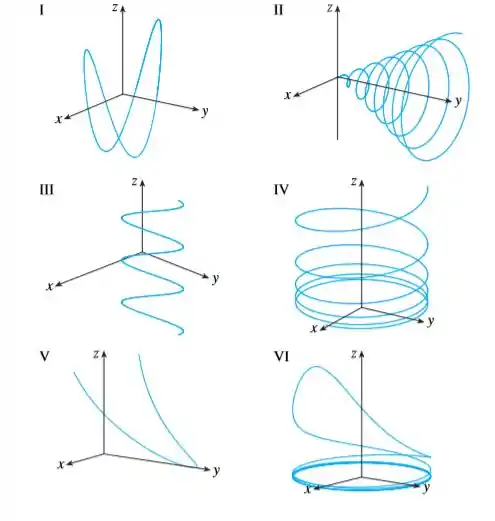
(Capítulo 13.1 – Exercício 21) Faça uma correspondência entre as equações paramétricas e os gráficos (identificados com números de I–VI). Justifique sua escolha.
Passo 1
Faaaaala galera!
Olha só, nesse exercício temos uma curva paramétrica e a imagem de 6 gráficos, e aí queremos saber qual desses gráficos corresponde à equação da curva que foi dada ok?
Para fazermos isso, vamos ter que analisar o comportamento da equação, vendo qual dos gráficos corresponde a esse comportamento
Boraaa
Passo 2
Temos
Legal, temos que a coordenada , logo o gráfico vai crescer ao longo do eixo 😉
Para as coordenadas e , como temos o seno em uma e o cosseno na outra, podemos pensar em algo envolvendo a relação trigonométrica fundamental:
Então vamos fazer:
Colocando em evidência:
Opa opa, isso é a equação de uma circunferência com raio . A coisa é que esse valor de não é fixo né, ele vai aumentando, pois
Então, no plano teremos uma espiral que começa com o raio zero e aumenta até infinito conforme t tende ao infinito.
Show, então analisando as figuras, verificamos que a única que contempla as análises feitas é a figura 2.
Resposta
Figura 2.