Agora precisamos tomar cuidado com o seguinte, o exercício novamente trata sobre interferência, porém agora a nossa interferência terá a componente de reflexão além é claro da componente de mudança de caminho. Vale relembrar que só temos mudança de fase quando ocorre uma reflexão de um raio luminoso que passaria de um meio menos refringente para um mais refringente, e sabemos que essa diferença de fase ser de π. Para entendermos melhor faremos o seguinte, no nosso desenho esquemático, os círculos representam a fase original e os quadrados a mudança de fase, com isso teremos que

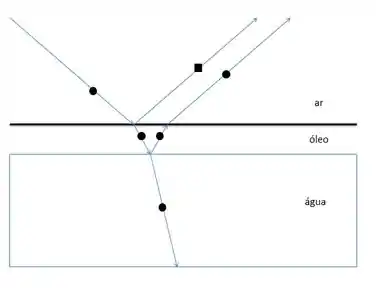
Só ocorre mudança de fase por reflexão na passagem do ar para o óleo, no caso da passagem do óleo para água não ocorre exatamente porque a água tem índice de refração menor que a do óleo.

Logo a diferença de fase por reflexão é

Agora temos que calcular a diferença de fase por caminho percorrido

Sabemos que a formula é

E nesse caso

Em que L é a espessura da camada de óleo

Também é importante lembrar que não temos o comprimento de onda no meio(

Apenas o comprimento de onda no vácuo, que é exatamente o que queremos determinar para saber quais comprimentos de ondas entram no intervalo estipulado pelo exercício, e podemos relaciona-los pela fórmula

Por fim queremos que a interferência de onda seja construtiva, ou seja, queremos que a nossa diferença de fase total seja um múltiplo de .

Agora vamos usar tudo isso para resolver a questão

Agora precisamos ver quais comprimentos de ondas fazem parte do espectro visível, que é exatamente o que o exercício pede.

Sabemos que o valor são

Agora vamos analisar cada valor de m

m=0

m=1

m=2

m=3

Com base nesse valores vemos que os únicos comprimentos de ondas presentes no espectro visível(400 a 700 nm) são