Em experimento com anéis de Newton o raio de curvatura da lente é 𝑅 = 6,0 𝑚 e seu diâmetro vale 𝑑 = 10 𝑚𝑚. O comprimento de onda é 589 𝑛𝑚. Admita que haja anéis de Newton até a borda da lente,
(a) Determine o número de anéis claros formados.
Passo 1
Nesse problema percebemos que como se trata de franjas claras e escuras, teremos que analisar as diferenças de fase por reflexão e por caminho percorrido.
Nosso objetivo é determinar a relação entre o raio da lente, o raio da franja, d, e claro a ordem da franja, só assim conseguiremos usar os valores do enunciado para achar o valor do número de franjas.
Passo 2
Analisando o desenho temos que ( lembrando que circulo significa uma fase e quadrado a mudança dela de um fator )
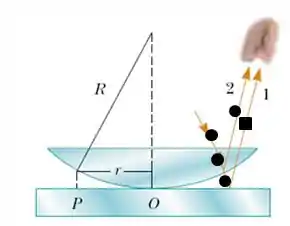
Analisando a imagem vemos que existe um raio com circulo e um raio com quadrado, o que significa que entre eles há uma diferença de fase de devido a reflexão da luz quando passa de um meio menos refringente para uma mais refringente.
Passo 3
A segunda coisa que temos que analisar é a diferença de caminho percorrido entre os raios, nesse caso sabemos que isso ocorre na região de medida d na figura, também já sabemos que a fórmula para diferença de fase por caminho percorrido é
Em que nesse caso o valor de
Passo 4
Por fim sabemos que a franja de ordem m, assim como a de ordem m+20 é clara, e é exatamente ela que temos que calcular. Mas lembra que quando temos uma franja clara significa que tivemos uma interferência construtiva, e quando temos interferência construtiva devemos calcular a nossa diferença de fase como uma múltiplo de , logo a nossa fórmula será
Agora vamos resolver o nosso exercício
Passo 5
Mudando os termos de lugar teremos
Feito isso podemos cortar os valores de ambos os lados da fórmula
Isolando o valor de teremos que
Passo 6
Agora que resolvemos a parte que relaciona as franjas precisamos da parte que relaciona as medidas do desenho para poder fazer a relação, olhando a figura com mais cuidado vemos que nela há um triangulo retângulo que podemos fazer Pitágoras.
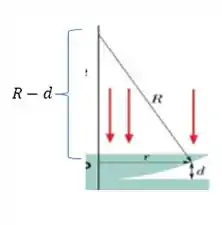
Fazendo Pitágoras teremos
Nessa equação podemos ignorar o valor de por ser muito pequeno, e também podemos cortar os valore de .
Sobra apenas
Isolando o nosso
Passo 7
Agora que temos duas fórmulas para podemos igualar eles
Isolando o valor de nessa equação teremos
Passo 8
Agora que já temos as fórmulas basta substituir os valores e calcular o valor de m, lembrando que esse valor não contabiliza o valor m=0, que será somado no final.
Substituindo na equação teremos que
Logo temos 6 franjas claras, mas sem contar a franja clara de m=0.
Logo o total de franjas claras serão
Logo o total de franjas claras será 7.
Resposta
7 franjas claras