Reflexão e Refração, Interferência
Um feixe de luz de comprimento de onda incide perpendicularmente sobre um filme fino de de espessura e índice de refração igual a .
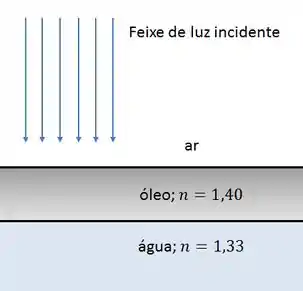
Parte da luz penetra no filme e é refletida na face interna inferior do filme.
- Calcule o número de comprimentos de onda contidos ao longo da trajetória da luz dentro do filme, desde o ponto de incidência até o ponto de saída da luz na face superior.
- Calcule a diferença de fase entre a onda refletida na face superior e a onda emergente proveniente da reflexão na face interna inferior.
Passo 1
Letra (a): Calcule o número de comprimentos de onda contidos ao longo da trajetória da luz dentro do filme, desde o ponto de incidência até o ponto de saída da luz na face superior.
Podemos relacionar os comprimentos de onda no ar e no óleo por:
Passo 2
Desde o ponto de incidência até o ponto de saída da luz na face superior, a luz percorre duas vezes a espessura da camada de óleo.
Assim, para sabermos o número de comprimentos de onda contidos ao longo da trajetória da luz dentro do filme , basta calcularmos:
Passo 3
Letra (b): Calcule a diferença de fase entre a onda refletida na face superior e a onda emergente proveniente da reflexão na face interna inferior.
A partir daqui, algumas informações são muito importantes para resolver esse tipo de problema.
- Se : Não há mudança de fase!
- Se : Há mudança de fase de meio ciclo !
Na parte superior, , logo, há mudança de fase de meio ciclo .
Para a onda emergente proveniente da reflexão na face interna inferior, , logo, não há mudança de fase.
Os dois raios já possuem uma diferença de fase de . Assim, a diferença de fase total será somada à diferença de fase relacionada à diferença de caminho.
Onde é a espessura da camada de óleo.
O comprimento de onda no óleo é dado por:
Onde:
;
;
Logo:
Passo 4
Onde:
;
;
Logo:
Resposta
Letra (a):
Letra (b):