Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Interferência em Filmes Finos

Ver Teoria
Exercício 38123456789101112131415161718192021222324252627282930313233343536373940414243444546474849505152535455

Enunciado

UFRJ, Física 4, P1 2017.2, 1

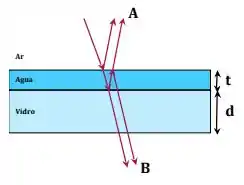
Um feixe de luz monocromático incide quase perpendicularmente em um filme fino de água de espessura t que está sobre um bloco de vidro de espessura d, como mostrado a figura. Dois observadores A e B determinam o respectivo critério para que a diferença de fase total dos raios emergentes leve a uma interferência CONSTRUTIVA. Considere a seguinte relação entre os índices de refração n a r < n v i d r o < n á g u a . De acordo com os observadores A e B, respectivamente, a interferência será CONSTRUTIVA quando (m e n são números inteiros positivos):

(a) 2 t = m + 1 2 λ a g u a e 2 d = n + 1 2 λ v i d r o

(b) 2 t = m λ a g u a e 2 d = n + 1 2 λ v i d r o

(c) 2 t = m + 1 2 λ a g u a e 2 t = λ a g u a

(d) 2 t = m λ a g u a e 2 t = n + 1 2 λ a g u a

(e) 2 d = m + 1 2 λ v i d r o e 2 t = n + 1 2 λ a g u a

(f) 2 d = m + 1 2 λ v i d r o e 2 d = n + 1 2 λ v i d r o

Passo 1

Sabemos que em interferências em filmes finos precisamos analisar diferença de fase por caminho percorrido e por reflexão quando passamos de um meio menos refringente para um mais refringente, dessa forma vamos fazer o seguinte, analisar o desenho para os momentos em que ocorrem mudança de fase por reflexão, em que o circulo é a fase inicial e o quadrado a mudança de fase.

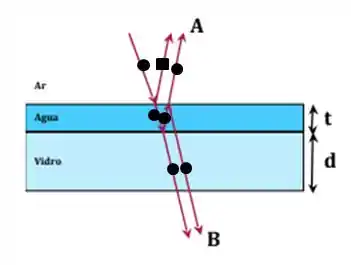
vamos fazer o seguinte, definir as diferenças de fases entre as reflexões para cada observador assim como as diferenças de fase por caminho percorrido.

Mas antes vamos tomar muito cuidado, perceba que nesse caso n v i d r o < n á g u a , logo nessa passagem de meio NÃO HAVERÁ mudança de fase por reflexão, sempre fomos acostumados que isso ocorre de forma contraria, mas como no enunciado isso foi definido dessa forma devemos tomar muito cuidado, sempre se lembre de garantir quais as relações entre os índices de refração. Nesse caso a única passagem em que ocorrerá mudança de fase por reflexão será do ar para o vidro, da água para o vidro NÃO OCORRERÁ pelos motivos que acabamos de falar.

Agora vamos partir pro cálculo

Passo 2

Para o caso de reflexões temos que,

Para o observador A

φ A = π

E para o observador B

φ B = 0

Para o caso de mudança de caminhos percorrido temos que,

Para o observador A

δ φ A =   2 t   .     2 π λ á g u a

Para o observador B

δ φ B =   2 t   .     2 π λ á g u a

Passo 3

Agora queremos que tenha interferência construtiva, para isso, sabemos que a interferência deve ser um múltiplo de 2 π , então, teremos as seguintes diferenças de fase para cada observador.

Para o observador B

2 t   .   2 π λ á g u a -   0 =   2 π n

2 t   .   2 π λ á g u a =   2 π n

2 t   λ á g u a =   n

2 t = n . λ á g u a

Para o observador A

2 t   .   2 π λ á g u a -   π =   2 π m

4 t λ á g u a -   1 π =   2 π m

4 t λ á g u a -   1 =   2 m

Isolando o valor de 2 t teremos

2 t = λ á g u a m +   1 2

Resposta

(c) 2 t = λ á g u a m +   1 2 (observador ponto A)

2 t = n . λ á g u a (observador ponto B)

Exercícios de Livros Relacionados

Exercício de Livro
Um filme de óleo com índice de refração de 1,45 flutua na água. Quando iluminado por luz branca em incidência normal, luz com comprimento de onda de 700n m e 500n m predomina na reflexão. Determine a
Um filme de óleo com índice de refração de 1,45 repousa sobre uma superfície de vidro opticamente plana que tem índice de refração de 1,60 . Quando iluminado com luz branca em incidência normal, luz c
Qual é a espessura mínima de uma película de sabão (excluindo o caso da espessura nula) para que se forme uma franja escura quando iluminada por luz de comprimento de onda igual a 480n m ? O índice de
Reflexão em filmes finos. Na Fig. 35-41, a luz incide perpendicularmente em um filme fino de um material 2 que está entre as placas (espessas) dos materiais 1 e 3. (Os raios foram desenhados com uma p