Interferência em Fendas Múltiplas e Películas Finas
Um filme de poliuretano com índice de refração é colocado sobre a superfície plana de um material com índice de refração .
Qual a espessura mínima do filme de poliuretano para que a luz de comprimento de onda de seja predominantemente refletida?
Caso a indústria te informe que não tem maquinário para produzir um filme tão fino, qual seria a próxima espessura que satisfaria o teu propósito?
e
e
e
e
e
e
e
Nenhuma das anteriores
Passo 1
Qual a espessura mínima do filme de poliuretano para que a luz de comprimento de onda de seja predominantemente refletida?
A situação é basicamente esta:
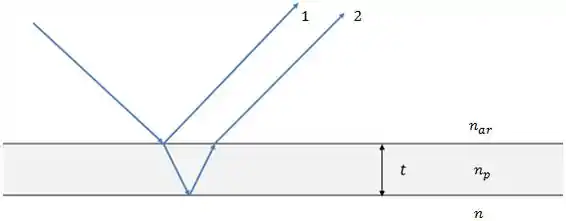
Assim, para que a onda seja predominantemente refletida, é necessário que os feixes 1 e 2 estejam em fase.
Passo 2
O primeiro feixe sofre uma reflexão vindo do ar indo ao filme fino que tem índice de refração , logo ele tem uma variação de fase por reflexão de .
Já o raio que entra no filme sofre uma reflexão vindo do material do filme que tem índice de refração indo para o material que índice . Como ele está indo do maior para o menor acaba não sofrendo nenhuma mudança de fase.
Assim a mudança de fase devido a reflexão entre os dois raios é
Já diferença de fase devido a diferença de caminho é dada por
Então a diferença de fase total é dada por
Passo 3
Como queremos uma interferência construtiva (raios em fase), então vamos ter que
Com
Assim igualando com a expressão do passo anterior
Isolando
Onde , e, como queremos a espessura mínima, vamos começar com . Logo:
Passo 4
Caso a indústria te informe que não tem maquinário para produzir um filme tão fino, qual seria a próxima espessura que satisfaria o teu propósito?
No outro caso, como queríamos a menor espessura, fizemos . Agora, como queremos a próxima, basta usar .
Substituindo os valores, teremos:
Resposta
e