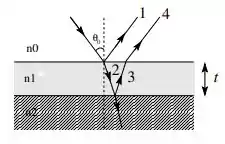
A figura abaixo mostra uma camada superior de índice de refração de espessura , depositada sobre uma camada espessa de índice de refração . O sistema está imerso em ar ). Luz monocromática com comprimento de onda , incide sobre a camada de espessura com um ângulo de incidência pequeno.
a) Determine as frequência e os comprimentos de onda da luz nos três meios.
b) Obtenha a mínima espessura da camada superior para que ela funcione como uma cama anti-reflexo (mínima reflexão) para este comprimento de onda em incidência normal.
c) Para a espessura calculada no item anterior, encontre os comprimentos de onda da luz visível () para os quais há um máximo de reflexão (interferência construtiva) para incidência normal.
Passo 1
Fala galera, vamos resolver mais uma prova da POLI? Essa primeira questão aqui é sobre interferência de ondas em filmes finos.
A luz, com comprimento de onda passa por outras dois meios com e . No item (a) queremos a frequência e o comprimento de onda em cada meio.
O principal conceito que você deve saber no item (a) é que a frequência de uma onda não é alterada quando ela sofre refração! Vamos calculá-la no ar:
Como a frequência não é alterada pela refração, ela é a mesma em todos os meios:
Passo 2
Para achar o comprimento de onda, lembre-se que o índice de refração é dado por
Como
Mas como vimos
Portanto,
Para achar o comprimento de onda num determinado meio, basta dividir o comprimento de onda do ar pela índice de refração do meio em questão. Assim,
Passo 3
Agora que temos os comprimentos de onda em cada meio podemos prosseguir no exercício! Note que parte do raio incidente é refletido logo na interface entre os meios (0) e (1): esse raio refletido é o raio 1. O raio refratado que passa para o meio (1) é o raio 2, que é refletido pelo meio (2) se tornando o raio 3 e que quando refrata de volta para o meio (0) passa a ser o raio 4. Eu sei que todo esse texto tá bem confuso, por isso leia ele com calma novamente, sempre identificando os raios na figura.
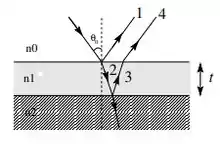
Queremos achar a menor espessura para que a interferência entre os raios 1 e 4 seja destrutiva dê origem a um mínimo de reflexão. Para que isso ocorra, a interferência entre os dois raios devem ser destrutiva! Vamos procurar a defasagem entre eles.
Na reflexão entre os meios (0) e (1), como , ocorre uma inversão na fase da onda. Da mesma forma, na reflexão entre os meios (1) e (2), também ocorre inversão de fase, pois . Assim, como a inversão ocorre nas duas reflexões, podem simplesmente desconsiderá-la: apenas a diferença de caminho é responsável pela defasagem!
Como estamos considerando incidência normal, a diferença de caminho é o dobro da espessura, já que a luz vai percorrer a espessura na “ida” e na “volta”:
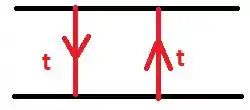
Você deve saber também que a defasagem é dada por
onde é o número de onda do meio (1). Assim,
Passo 4
Para que a interferência seja destrutiva, devemos ter
Assim,
Como :
O exercício quer a menor espessura, então você precisa tomar :
Passo 5
Vamos pro último item! Ele pede para usarmos como espessura e procurar o comprimento de onda para que a interferência seja construtiva. Já sabemos que a defasagem é
Como a interferência deve ser construtiva, temos
Assim, Muita coisa em uma linha só na equação abaixo. Melhor pular linha do que ir fazendo um ao lado do outro. E deixar o que se quer, no final, por exemplo, uma linha escrita só com lamba0=300/m nm
Portanto,
Substituindo os valores:
Assim,
O problema pediu para acharmos na faixa visível (). Mas para qualquer valor possível de , teremos
Sendo assim, não existe no visível tal que a interferência seja construtiva se .
Com isso terminamos o problema 😊!
Resposta
a)
b)
c) Não existe.