Um raio de luz monocromática incide perpendicularmente em um filme fino de água de espessura , sobre um bloco de vidro de espessura como mostrado na figura abaixo.

Dois observadores, e , determinam o critério para que a diferença de fase total dos raios emergentes leve a uma interferência destrutiva.

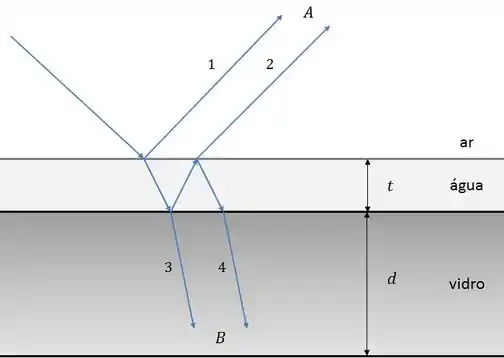
De acordo com os observadores e, respectivamente, a interferência será destrutiva quando:

1. ;
2. ;
3. ;
4. ;
5. ;
6. Nenhuma das anteriores

Vamos analisar o problema de dois pontos de vista diferentes, ok?

Observador :

Para o raio chegar ao observador ele é apenas refletido na superfície da água.

Já para o raio chegar ao observador , inicialmente ele é refratado quando passa pela superfície da água e refletido quando incide sobre a superfície do vidro, passando para o ar novamente ao incidir sobre a superfície da água.

Assim, a diferença de caminho é dada por:

E como essa diferença de caminho se refere quando o raio está na água, temos que usar o comprimento de onda dessa luz na água

Como os dois raios sofrem uma reflexão, cada, ambos estão em fase.

Do ponto de vista do observador , para que os dois raios sofram interferência destrutiva, é necessário que a diferença de caminhos entre eles seja dada por:

Logo:

Ou reescrevendo o comprimento de onda como

Essa condição por ser também

Em nenhuma das opções da questão aparece , por isso usamos direto a forma com .