Uma onda eletromagnética de comprimento de onda λ = 600 nm .incide sobre um dispositivo de interferência tipo Young. Após as duas fendas saem duas ondas em fase que se superpõem em uma tela de observação distante produzindo interferência. Na saída de uma das fendas coloca-se uma placa de Mica com índice de refração n = 1,58 e espessura X. Em consequência ocorre um deslocamento do padrão de interferência por 7 máximos sucessivos para o lado onde foi colocada a placa de Mica. Determine a espessura X dessa placa de Mica.
Passo 1
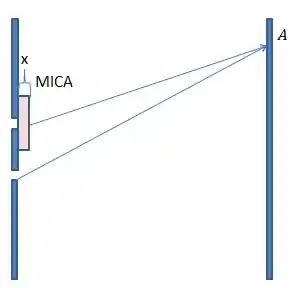
Nessa questão precisamos compreender o problema visualmente.
Vemos pela figura que nesse caso teremos interferências em filmes finos, sendo nesse caso interferência em uma placa fina de mica.
Sabemos que um dos motivos de ocorrer mudança de fase em filmes finos é causado pela diferença de caminho percorrido. Já conhecemos a fórmula que é dada por
Para a fenda com a barra de mica teremos que a diferença de fase por caminho percorrido será
Aqui vale ressaltar que o comprimento de onda dado no enunciado é o comprimento de onda no vácuo, mas como na fórmula está o da mica faremos então a mudança seguindo a seguinte fórmula
Substituindo na fórmula teremos
Passo 2
Para a fenda sem a barra de mica teremos que a diferença de fase por caminho percorrido será
Passo 3
Além disso sabemos que a interferência é construtiva pois temos uma franja clara, logo, isso significa que a nossa diferença de fase total por caminho percorrido deve ser um múltiplo de , logo a nossa fórmula será
Cortando o
Isolando x teremos
Sabemos que os dados são
E também sabemos que o máximo central sofreu um deslocamento de 7 franjas, ou seja, agora nosso máximo central é em m=7
Passo 4
Substituindo os valores teremos