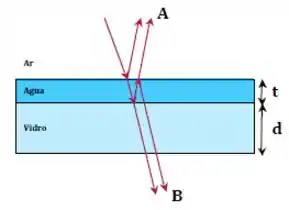
Um raio de luz monocromático incide quase perpendicularmente em um filme fino de água de espessura , sobre um bloco de vidro de espessura , conforme figura abaixo.

Dois observadores, e , determinam o critério para o qual a diferença de fase total, por reflexão e/ou caminho ótico percorrido dos raios emergentes, leve a uma interferência destrutiva.

Considere . De acordo com os observadores e , respectivamente, a interferência será destrutiva quando ( e são números inteiros positivos):

,

1. e
2. e
3. e
4. e
5. e
6. e

Para o observador , a diferença de fase por reflexão vai ser zero, pois um raio sofre mudança de fase ao refletir na interface ar-água, e o outro raio sofre mudança de fase ao refletir na interface água-vidro. Assim:

Logo, a diferença de fase é devida apenas ao caminho percorrido. A condição para interferência destrutiva vai ser:

Como o observador é o contrário do observador , então a condição para interferência destrutiva fica:

Esse passo é pra quem não curtiu muito o “pulo do gato” que eu dei antes. Sem problemas, podemos fazer etapa por etapa.

Pra começar, vamos olhar BEEEEM de perto o filme de água.

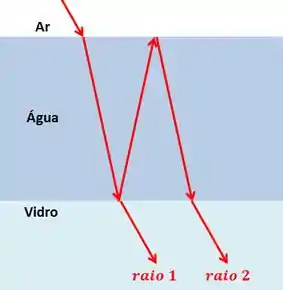
Vamos olhar a diferença de fase por caminho:

O raio 2 percorre um caminho , enquanto o raio 1 percorre um caminho . Logo, teremos:

Agora olhemos a diferença de fase por reflexão:

O raio 1 não é refletido, então não sofre diferença de fase por reflexão. Já o raio 2 reflete na interface água-vidro, sofrendo uma mudança de reflexão , e depois ela reflete na interface água-ar, incidindo da água no ar e, como , ela não sofre mudança de fase. Logo:

A diferença de fase total é a soma dos dois.

Pra termos interferência destrutiva, .