Um feixe de luz plana monocromática, viajando no ar, incide sobre uma placa de Zircônio, cujo índice de refração é .
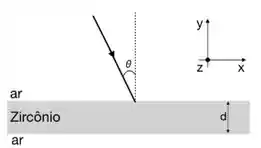
a) Seja o ângulo de incidência . Qual de propagação da luz dentro do Zircônio? Escreva em termos dos vetores unitários , e , de acordo com o sistema de coordenadas mostrado na figura).
b) Suponha que a espessura da placa de Zircônio seja . Se a luz parte de uma posição acima da face superior da placa, quanto tempo leva para emergir na face inferior da placa?
c) Seja agora (incidência normal) e a espessura da placa de Zircônio . Para quais comprimentos de onda dentro do espectro visível a intensidade da luz refletida (emergindo pela face superior da placa) é nula?
Passo 1
Eai galerinha, bora resolver mais uma questão de física 4!
Nos dois primeiros itens vamos considerar apenas a refração da luz entre o ar e o filme de Zircônio:

Primeiro vamos usar a lei de Snell para achar o ângulo de refração:
Como , e , temos que
Com isso, podemos achar também
O enunciado pede para acharmos o versor que dá a direção de propagação do raio refratado. Fazendo a decomposição:
Portanto,
Passo 2
No item (b) queremos saber o tempo que demora para a luz percorrer todo o caminho. No ar ela percorre uma distância e no Zircônio uma distância . Olhando para os triângulos retângulos:
No ar a velocidade da luz é , de modo que
Já no Zircônio, a velocidade de propagação é
Portanto,
Daí é só somar os tempos:
Ou ainda,
Passo 3
Por fim, vamos ao item (c)! Agora vamos discutir sobre interferência em filmes finos!
Vamos considerar a seguinte situação:
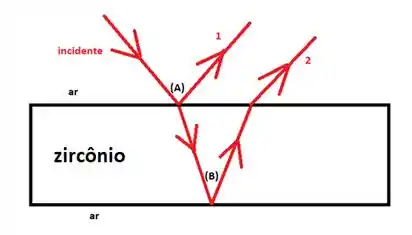
PS: o problema disse que a incidência era normal, porém representei ela inclinada para ficar mais fácil de visualizar a situação. Mas tenha em mente que todos esses raios deveriam estar desenhados na vertical!
A luz incidente sobre o cristal é parcialmente refletida (raio 1) e parcialmente refratada. A parte refratada será refletida em (B) na interface entre o cristal e o ar e depois retornará para o ar (raio 2). Os raios 1 e 2 vão interferir destrutivamente de modo que não será observada luz refletida. O exercício quer que achemos a espessura da placa para que isso ocorra!
Para fazer isso, temos que calcular a diferença de fase entre os raios 1 e 2. Essa diferença de fase terá duas contribuições!
A primeira contribuição vem do fato de haver inversão de fase na reflexão (A) mas não haver inversão na reflexão (B). Isso significa que devemos somar um fator na defasagem! Lembre-se que a inversão de fase ocorre quando a reflexão ocorre de um meio com índice de refração menor para um meio com índice de refração maior!
A outra contribuição vem da diferença de caminho. Nesse caso, a diferença de caminha do raio 2 com relação ao raio 1 é simplesmente o dobro da espessura da placa:
Com todas essas informações, temos que a diferença de fase é
A defasagem devido a diferença de caminho é o número de onda vezes a diferença de caminho e somamos o fator devido a inversão de fase na reflexão (A)! Usando que
temos que
Passo 4
O exercício forneceu o comprimento de onda da luz no ar . Como relacionar isso com o comprimento da luz na placa de Zircônio? A boa e velha refração!
Sabemos que quando uma onda refrata, sua velocidade e comprimento de onda mudam, porém sua frequência é inalterada. Desta forma,
Lembre-se que e que no ar é a velocidade da luz no vácuo! Assim, temos que
pois . Substituindo isso na relação para a defasagem:
Passo 5
Estamos quase acabando, falta pouco!
Para que a interferência seja destrutiva, devemos ter
Isso significa que a defasagem deve ser um múltiplo ímpar de . Portanto,
Logo,
Daí, vamos substituir e :
A faixa do visível vai de até :
Logo, temos que achar os valores de que satisfazem
Portanto, achamos
Vemos que os possíveis de são
Assim,
Com isso, os comprimentos de onda dentro do visível para que a interferência seja destrutiva são
Isso fecha o problema 😊!