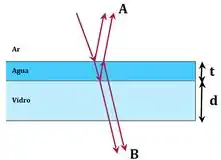
Um raio de luz monocromático com comprimento de onda , no ar, incide quase-perpendicularmente em um filme fino de água de espessura , sobre um bloco de vidro de espessura , como mostra a figura fora de escala abaixo. Sabendo que os índices de refração de cada meio valem, respectivamente, , e , determine um valor de para que a interferência em seja construtiva.
Passo 1
Primeiro, vamos revisar, bem rápido, a ideia física que está por detrás do problema. A luz vem e incide sobre a interface ar-água e parte dessa onda é refletida e outra parte é refratada para o meio onde tem água e que tem espessura .
Essa onda refratada atinge agora a interface água-vidro, que tem espessura , e parte dela também é refletida. Quando esta onda refletida se junta àquela refletida na interface ar-água (espessura ) e se combinam, pode haver interferência construtiva ou destrutiva, dependendo da diferença de caminho entre as ondas refletidas.
Como em ambas as interfaces a luz está vindo de um meio cujo índice de refração é menor do que o índice de refração do meio seguinte, então as ondas refletidas em cada uma das interfaces estarão defasadas de .
Por isso, para que haja interferência construtiva, devemos ter o seguinte
ou seja, a diferença de caminho deve ser um múltiplo inteiro do comprimento de onda da luz dentro da água.
Passo 2
O nosso objetivo é encontrar um valor do comprimento de onda para que haja a interferência construtiva em . Quando a luz entra na água, seu comprimento de onda mudará e é esse novo comprimento de onda que teremos que considerar.
O comprimento de onda é dado por
Jogando na expressão do Passo 1, junto com os valores que o problema fornece, teremos
Agora, como é um número inteiro, vamos ter vários comprimentos de onda para os quais teremos interferência construtiva no ponto .
Para ,
Para os outros valores do inteiro , teremos valores de comprimentos de onda que não estão em nenhuma das alternativas que o problema mostra.
Resposta
Letra d).