Uma película especial, com índice de refração , é projetada para aumentar a refletividade da radiação solar. A película é fixada na parte de fora de um vidro com índice de refração .
Qual deve ser a espessura mínima da película para diminuir a transmissão da radiação no infravermelho ()?
Passo 1
Como estamos falando de transmissão, teremos o seguinte caso:
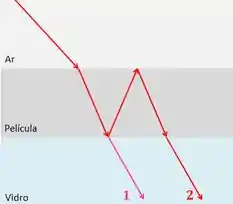
Se a película tiver uma espessura , então a diferença de fase por causa do caminho vai ser:
Já por reflexão, teremos que o raio não vai sofrer nenhuma reflexão, enquanto o raio também não (visto que e que ).
Diferençe de fase total vai ser então:
Passo 2
Como queremos diminuir a transmissão da radiação, queremos então que:
Igualando, teremos:
A espessura mínima vai corresponder a .
Pelo enunciado, e , logo:
O que corresponde com a letra (a), .
Pode parecer estranho não ter batido de forma exata, mas provavelmente foi utilizado um valor ligeiramente diferente pro comprimento de onda, visto que é um valor exato.
Se usassemos , o valor daria aproximadamente o da prova, . E isso é bem próximo do nosso, .
Resposta
Letra (a)