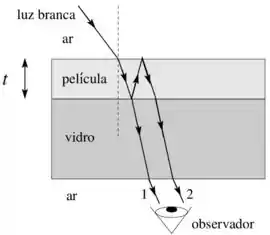
Uma película transparente de espessura e com índice de refração está colocada entre dois meios dielétricos: ar (índice de refração ) e vidro (índice de refração ). Luz branca incide quase normalmente sobre essa película e um observador vê a luz transmitida, conforme a figura. A luz branca tem comprimentos de onda entre e . Para quais comprimentos de onda neste intervalo haverá interferência construtiva entre os raios e da figura?
Passo 1
Vamos agora analisar a diferença de fase entre os raios e . Se essa diferença for um múltiplo de teremos a interferência construtiva.
Vamos então olhar para o raio . A diferença de fase dele com o raio acontece devido a dois fatores : diferença de caminho ótico na película e reflexões sofridas pelo raio , de forma que
Passo 2
Vemos pela figura que o raio sofreu duas reflexões: a primeira vindo da película para o vidro e a segunda vindo da película indo para o ar.
Como o índice de refração da película () é maior do que o do ar ( e menor do que a do vidro (), temos que somente na primeira reflexão haverá uma mudança de fase. Assim:
Passo 3
Agora vamos olhar para a diferença de fase devido à diferença de caminho. Como o raio incide quase perpendicular temos que devido as duas reflexões o raio percorrerá na película uma distância a mais que o raio . Assim teremos que
Onde
é o comprimento de onda do raio dentro da película. Agora temos de vez que
Passo 4
Agora que temos todas as contribuições para a diferença de fase, podemos avaliar para quais comprimentos de onda podemos ter interferência construtiva
,
Isolando o comprimento de onda da luz nessa expressão temos:
Substituindo os dados da questão e vendo os possíveis valores de descobrimos alguns possíveis comprimentos de onda que têm interferência construtiva
Como os comprimento na luz branca estão entre e , vemos que nesse caso não há como ter interferência construtiva para estes comprimentos de onda.
Resposta
nesse caso não há como ter interferência construtiva para estes comprimentos de onda.