Reflexão e Refração, Intensidade
O vidro de um carro, com índice de refração é coberto por fora por uma película fina com índice de refração tal que .
Uma luz monocromática proveniente do exterior do carro incide no vidro quase perpendicularmente ao mesmo.
Se é o comprimento de onda desta luz dentro da película, quão fina deve ser a película para que haja luz refletida?
(Considere a interferência entre os raios provenientes das superfícies ar-película e película-vidro)
- Nenhuma das anteriores
Passo 1
Temos a seguinte situação:
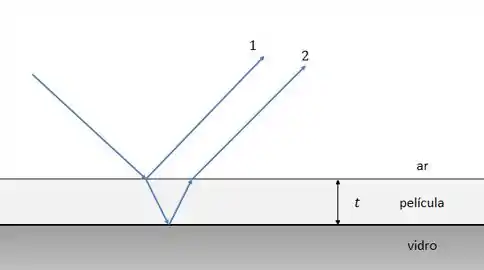
Para que haja luz refletida é necessário que haja interferência construtiva entre os raios 1 e 2. Isso acontece quando a diferença de fase entre esses dois raios é
Passo 2
O raio de luz dentro da película percorre o caminho aproximadamente igual a . A diferença de fase devido a diferença de caminho ótico vai ser dada por
Onde é o comprimento de onda na película como o enunciado pediu para considerar.
Passo 3
O raio ao refletir na superfície ar-película sofre uma mudança de fase por reflexão de .
Já o raio 2 ao refletir na superfície película-vidro também sofre uma mudança de fase por reflexão de .
Assim a diferença de fase por reflexão entre os dois raios é 0, já que os dois mudaram a mesma coisa!
Passo 4
Assim a diferença de fase total entre os dois raios é
Usando a condição de interferência construtiva
Logo:
Pegando o primeiro caso
Resposta
Letra (b):