Física 4 – UFRJ – 2019.1 – PF – Questão 8
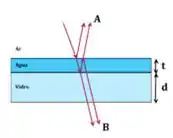
Um raio de luz monocromática incide quase perpendicularmente em um filme fino de água de espessura , sobre um bloco de vidro de espessura , como mostra a figura abaixo. Se os índices de refração dos meios satisfazem , pode-se concluir que a interferência em A será construtiva:
a) com , na qual é um número natural e , o comprimento de onda da luz na água.
b) com , na qual é um número natural e , o comprimento de onda da luz na água.
c) com , na qual é um número natural e , o comprimento de onda da luz no ar.
d) com , na qual é um número natural e , o comprimento de onda da luz no ar
Passo 1
Fala pessoal, beleza?
Esse é um problema sobre interferência em filmes finos. A grande sacada do problema é achar a defasagem entre os raios no ponto A.
A raio refletido entre o ar e a água sofre inversão de fase pois . Da mesma forma, o raio refletido entre a água e o vidro também sofre inversão, já que . Como os dois raios sofrem inversão, isso não será relevante para o problema.
Desta forma, a diferença de fase entre os raios será dada simplesmente pela diferença de caminho. O raio que passa pela água vai percorrer uma distância extra com relação ao raio que só se propaga no ar. Com isso, a defasagem será
Lembre-se também que o número de onda é dado por
Assim,
Passo 2
Para que a interferência seja construtiva, a defasagem deve ser um múltiplo inteiro de :
Assim,
Logo,
Essa é a condição de interferência construtiva, que é mostrada na alternativa A 😊.
Resposta
Alternativa A.