Luz monocromática de comprimento de onda incide sobre uma fenda . Um espelho metálico plano está a uma distância abaixo de , muito menor do que a separação entre a fenda e a tela.
Na tela aparecem faixas claras e escuras devido à interferência entre as ondas que partem de e atingem a tela diretamente e via reflexão no espelho.
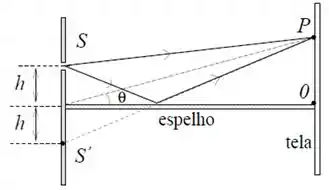
- Contrariamente à experiência de Young, a franja para no ponto da tela é escura. Explique a diferença.
- Deduza a condição que o ângulo deve satisfazer para haver interferência construtiva entre as ondas diretas e refletidas no ponto da tela. Observe que o raio refletido percorre a mesma distância que o raio que parte da imagem virtual da fenda no espelho (veja a figura).
Passo 1
Letra a)
Para um dado ponto qualquer na tela, a interferência da luz irá se dar por duas fontes de diferença de fase:
A diferença de caminho entre o raio que vai de diretamente a e o raio que é refletido no espelho.
A mudança de fase de (meio comprimento de onda) sofrida pelo raio que se reflete no espelho metálico.
A medida que aproximamos o ponto do centro da tela, a diferença de caminho vai tendendo a zero, sem termos diferença de fase por isso.
Porém, ainda teremos uma diferença de fase de por causa da reflexão.
Essa diferença corresponde a uma interferência destrutiva e, por isso, o meio da tela corresponde a uma franja escura.
Passo 2
Letra b)
A diferença de fase entre os dois raios é de:
Onde
A diferença de fase por caminho é a mesma que no experimento de Young tal que a distância entre as duas fendas seja , pois o raio refletido percorre a mesma distância que a imagem especular S’ da fenda S, semelhante a um experimento de Young. Com isso:
Logo, a diferença de fase total será:
Passo 3
Para que tenhamos interferência construtiva, é necessário que
Substituindo:
Resposta
Letra a)
Há uma diferença de fase de por causa da reflexão.
Essa diferença corresponde a uma interferência destrutiva e, por isso, o meio da tela corresponde a uma franja escura.
Letra b)