Um filme fino de espessura t variável e índice de refração n2 é iluminado por luz
monocromática de comprimento de onda que no vácuo é igual a . O filme encontra-se
imerso em um meio cujo índice de refração . Observa-se a interferência
dos raios 1 e 2 provenientes da reflexão da luz nas superfícies superior e inferior do
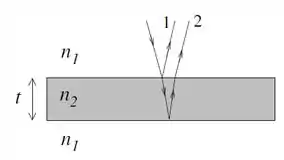
filme, conforme a figura. Considere incidência normal.
a)Calcule o valor a mínimo da espessura do filme para que a intensidade
da luz observada seja máxima.
b)Calcule o valor b mínimo da espessura do filme para que a intensidade da luz observada seja mínima.
Passo 1
Nesse caso estamos analisando a interferência em filmes finos e nesse primeiro caso o nosso objetivo é o seguinte.
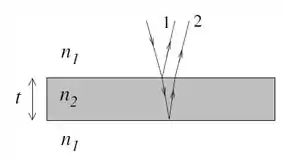
Qual deve ser a espessura do nosso filme para que a interferência entre os nossos raios observados seja máximo.
Vamos lembrar o seguinte, sempre que um raio de luz passa de um meio com índice de refração menor para um maior, na reflexão teremos mudança de fase, nunca na refração e nunca quando passamos de um meio mais refringente para um menos refringente, então se chamarmos de uma fase e de a mudança, teremos.
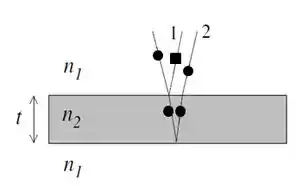
Logo pela figura sabemos que entre os raios 1 e 2 temos uma diferença de fase, que por reflexão sempre é dado por um fator
Também precisamos lembrar que a variação de fase por caminho é dada por
Em que é a variação de caminho entre as luzes, para o raio 2 teremos
Pelo desenho vemos que o raio 1 sofre uma diferença de fase por reflexão, exatamente por ser pela passagem de uma meio mais refringente para um mais refringente.
Passo 2
Mas pensa no seguinte, queremos que essas ondas sejam construtivas, logo a diferença de fase por reflexão e por caminho percorrido deve ser um múltiplo de , com isso a diferença de fase será dada pela fórmula
Isolando o valor de teremos
Mas antes de tudo tome o seguinte cuidado, pois o comprimento de onda dado no enunciado se refere ao comprimento de onda no vácuo, enquanto que o que está na fórmula se refere ao comprimento de onda no meio, mas fique tranquilo, sabemos que
Logo
Substituindo esse valor na nossa conta teremos que
Como queremos a espessura mínima, então faremos m=0
Passo 3
Na letra b queremos que a espessura seja mínima, mas agora com uma interferência destrutiva.
Sabemos que a diferença de fase por caminho percorrido é dada por
E que a diferença de fase devido a reflexão de um meio menos refringente para uma mais refringente é
Mas como já foi mencionado, essa variação deve ser destrutiva. Mas pensa comigo, se para ser construtiva deve ser um múltiplo de para ser destrutiva deverá ser um múltiplo de .
Mas aqui devemos tomar o seguinte cuidado, pois para ser múltiplo de não basta apenas fazer pois para o caso de a interferência seria construtiva.
Logo a forma correta de fazermos um múltiplo de é da seguinte maneira
Pois nesse caso, independente do valor de teremos múltiplos de .
Passo 4
Vamos agora resolver o problema do nosso exercício pois sabemos que a diferença de fase deve ser um múltiplo inteiro de , usando o que já sabemos sobre o caminho percorrido e a diferença de fase termos.
Isolando o valor de teremos
Lembrando de trocar
Teremos que
como queremos a espessura mínima faremos m=0
Resposta
a)
b)