Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução e Definição de Integral

Ver Teoria
Exercício 61234578910111213141516171819202122232425262728293031323334353637383940

Enunciado

USP – Sem Campus –Cálculo 2 – Provas Antigas – P1 - 2022.1 – 2

Calcule a área da região limitada pela curva x y = 1 e abaixo das retas y = x e x + 2 y = 4 .

Passo 1

Fala aí galerinha? Tudo bem com vocês? Bora pra cima! Primeiro, pra uma questão bem feita, vamos desenhar a área que precisamos calcular.

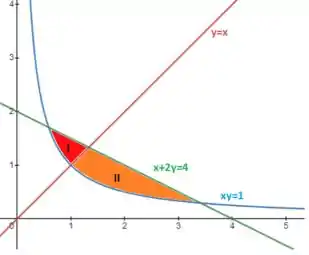
Ela é essa pintada em azul. Dividimos em 2 áreas, pois vamos precisar de dois cálculos para acharmos a área. Isso acontece porque em um momento, a parte de cima da área é definida por y = x e depois é definida por x + 2 y = 4 . Então dividimos no ponto B. E ela vai até o ponto C onde encontra a curva = 1 . Próximo passo é calcular os pontos aonde essas funções se encontram.

Passo 2

Passo 3

Encontrando os pontos, vamos primeiro pro ponto A. Nele quem se tocam são as funções

x y = 1   ( 1 )

y = x   ( 2 )

Aplicando (2), em (1), temos:

x ⋅ x = 1

x 2 = 1

x = ± 1

Aplicando de volta em (2):

y = ± ( 1 )

Logo o ponto é:

x , y = ( 1,1 )

Para o nosso caso em que estamos trabalhando no primeiro quadrante, vamos adotar os valores positivos para x   e y .

Para o ponto B, quem se tocam são as funções:

y = x

x + 2 y = 4

Analogamente para o ponto A:

x + 2 x = 4

x = 4 / 3

y = 4 / 3

Portanto, o ponto de toque é:

x , y = 4 3   , 4 3

Por fim para o ponto C, quem se toca lá é:

x y = 1

x + 2 y = 4

O procedimento vocês já sabem né? Vamo isolar y na primeira eq:

y = 1 x

Aplicando na segunda eq:

x + 2 x = 4

x 2 + 2 = 4 x

x 2 - 4 x + 2 = 0

Temos que as raízes são:

x = 2 ± 2

E como estamos trabalhando no primeiro quadrante, adotaremos o valor positivo para x. Logo,

x , y = 2 + 2 , 2 - 2 2

Passo 4

Portanto agora que temos tudo armadinho, vamos montar nossa integral:

A área total é dada por:

A = A I + A I I

A área I é dada por:

∫ 1 4 / 3 x - 1 x d x

A área I I é dada por:

∫ 4 / 3 2 + 2 2 - x 2 - 1 x d x

Logo,

A T = ∫ 1 4 / 3 x - 1 x d x + ∫ 4 / 3 2 + 2 2 - x 2 - 1 x d x

Agora vamos resolver, temos:

A T = x 2 2 + l n l n   x   1 4 / 3   + 2 x - 2 x 2 4 - l n l n   x   4 3 2 + 2  

A T = 0,601 + 0,5 + [ 2,686 - 1,935 ]

A T = 0,853   U a

Resposta

A T = 0,853   U a

Exercícios de Livros Relacionados

Encontre ∫ 0 5 f x d x se f x = 3 p a r ax3 xp a r ax ≥ 3
7. Calculea ) int_0^((pi)/(8)) cos^2 x d x
Nos Exercícios 51-54, use uma integral definida para determinar a área da região entre a curva dada e o eixo x no intervalo [ 0 ,b ] .52. y = π x ² ²
Encontre ∫ 0 5 f x d x se f x = 3 ,     p a r a   x3 x ,     p a r a   x ≥ 3
Suponha que f tenha uma valor mínimo absoluto m e um valor máximo absoluto M . Entre quais dois valores ∫ 0 2 f x d x deve ficar? Que propriedade das integrais lhe permitem tirar esta conclusão?