Exercícios Resolvidos de Introdução e Definição de Integral

Enunciado

Pessoal, vamos usar a mesma estratégia de integração:

Nesse intervalo de integração da função já temos alguns valores:

Podemos dividir esse intervalo em partes, então teremos que cada pequena partição será o valor final menos o inicial dividido por :

Ficamos com:

E olhando para dentro do nosso somatório, precisamos definir quais são os valores de :

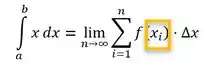
E vamos calcular cada um dos valores de da seguinte forma:

Logo substituindo os nossos valores:

Agora pensando na função , podemos pegar a função que está sendo utilizada dentro da integral:

E substituindo o valor de que acabamos que calcular:

Hora de voltarmos ao somatório com todo esse grupo de informações que levantamos belamente:

Substituindo nossos valores:

Já ta craque nesse passo né? Hora de continuar resolvendo o somatório dentro do limite:

Pela série geométrica, nós calculamos que:

Fazendo esse produto:

Chegamos em:

Voltando para a integral:

Substituindo:

Novamente, a dica é jogar todos os valores que independem de para fora do limite:

Simplificando os numeradores e denominador dentro do limite:

Esse limite retorna o valor:

Substituindo no cálculo da integral:

Pode gritar que você venceu! Chegamos no final da questão!