Calcule a partir da definição as seguintes integrais:
a)
Passo 1
Fala aí, gente bonita! Esse enunciado está nos pedindo para calcular uma integral através da sua definição, então vamos precisar falar sobre somatórios de intervalos da função!
Lembra dessa definição aqui:
Primeiro temos vamos lembrar qual é o intervalo de integração da função:
Podemos dividir esse intervalo em partes, então teremos que cada pequena partição será:
E olhando para dentro do nosso somatório, precisamos definir quais são os valores de :
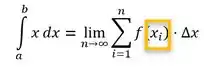
E vamos calcular cada um dos valores de da seguinte forma:
Nesse nosso caso, podemos substituir o valor de que já foi calculado:
Agora pensando na função , podemos pegar a função que está sendo utilizada dentro da integral:
E substituindo o valor de que acabamos que calcular:
Ótimo, parabéns por chegar até aqui, agora é hora de voltarmos ao somatório com todo esse grupo de informações que levantamos:
Substituindo nossos valores:
Passo 2
Vamos resolver esse limite para igualar a integral:
Você concorda comigo que o elemento está apenas multiplicando a parcela que depende de , então como o somatório está variando o valor de entre e , podemos passar essa parcela multiplicativa pra fora:
Como a parcela não depende de , podemos jogar ela pra fora do limite que depende de :
Agora olhando para dentro do somatório, pela propriedade da aditividade, podemos quebrar o somatório em duas partes:
Sabemos que o somatório de uma constante é igual a constante multiplicada pelo valor do número de parcelas, nesse caso :
Enquanto o podemos passar todos os valores que estão multiplicando a variável do somatório para fora:
Então nossa equação se torna:
O somatório de uma variável que está crescendo de até é igual a:
Logo, podemos substituir o nosso último somatório como:
Simplificando o produto entre as duas expressões, temos:
Podemos simplificar ainda mais dividindo as parcelas dentro do colchetes por :
E assim podemos aplicar o limite em duas parcelas que se somam:
Todo mundo que não varia com podemos jogar para fora do limite:
Então quando tendemos o valor de até o infinito, o limite nesse caso é igual a :
Nosso caso se torna:
Agora juntando tudo em uma mesma fração:
Pelo produto notável encontramos que nossa integral que queríamos calcular desde o início é igual a:
Resposta
a)