Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução e Definição de Integral

Ver Teoria
Exercício 13123456789101112141516171819202122232425262728293031323334353637383940

Enunciado

Q02c) Calcule as seguintes integrais:

∫ - π π sin ⁡ x   d x

Passo 1

Não sei você mas quando eu vejo um módulo já fico preocupado. E agora, o que fazer? Bem já que módulo atrapalha a gente nas contas, vamos retirar ele! Pra lembrar, da definição de módulo, temos:

f x = f x   ,     f x ≥ 0 - f x ,     f x < 0

Aplicando isso pra f x = sin ⁡ x , vamos ter:

sin ⁡ x = sin ⁡ x   ,     sin ⁡ x ≥ 0 - sin ⁡ x ,     sin ⁡ x < 0

Ok, mas como isso ajuda a gente. Bem, temos que ver quando que sin ⁡ x ≥ 0 e quando que sin ⁡ x < 0 . Vamos conversar então com nosso amigo círculo trigonométrico:

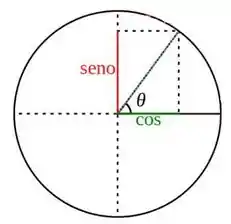
Olha só, enquanto o ângulo está entre 0 º e 180 º = π , o seno é positivo! Entre 180 º = π e 360 º = 2 π , o seno passa a ser negativo. Como isso vale só pra uma volta, podemos expandir a ideia pra mais de uma, mas nem precisamos. Veja bem os limites de integração:

∫ - π π sin ⁡ x   d x

A integral está indo de - π a π não é? Então vou fazer o seguinte, vou separar essa integral em duas:

∫ - π π sin ⁡ x   d x = ∫ - π 0 sin ⁡ x   d x + ∫ 0 π sin ⁡ x   d x

Agora fica mais claro de a gente ver. Saca só, na primeira integral, pro círculo trigonométrico, temos:

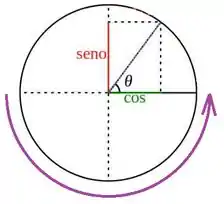
Opa, não são esses os quadrantes do círculo trigonométrico onde o seno é negativo? Sendo assim, nesse intervalo:

sin ⁡ x = - sin ⁡ x

Agora pra outra integral, vamos ter no círculo trigonométrico:

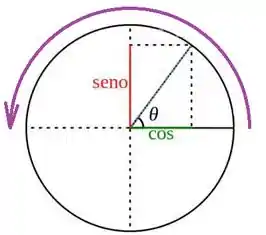
Nesse intervalo então:

sin ⁡ x = sin ⁡ x

A integral do enunciado pode ser reescrita para:

∫ - π π sin ⁡ x   d x = - ∫ - π 0 sin ⁡ x   d x + ∫ 0 π sin ⁡ x   d x

Passo 2

Agora é só calcular mesmo, sem mistério. As duas integrais são iguais, mudando só o sinal, então o resultado delas é o mesmo, beleza? Como a função que eu tenho que derivar pra achar seno é menos cosseno, vamos ter:

∫ - π π sin ⁡ x   d x = - ∫ - π 0 sin ⁡ x   d x + ∫ 0 π sin ⁡ x   d x

∫ - π π sin ⁡ x   d x = - - cos ⁡ x x = - π x = 0 + - cos ⁡ x x = 0 x = π

∫ - π π sin ⁡ x   d x = - - cos ⁡ 0 - - cos ⁡ - π + - cos ⁡ π - - cos ⁡ 0

Substituindo os valores dos cossenos:

∫ - π π sin ⁡ x   d x = - - 1 - 1 + 1 - - 1

∫ - π π sin ⁡ x   d x = - - 2 + 2 = 2 + 2 = 4

Resposta

∫ - π π sin ⁡ x   d x = 4

Exercícios de Livros Relacionados

Encontre ∫ 0 5 f x d x se f x = 3 p a r ax3 xp a r ax ≥ 3
7. Calculea ) int_0^((pi)/(8)) cos^2 x d x
Nos Exercícios 51-54, use uma integral definida para determinar a área da região entre a curva dada e o eixo x no intervalo [ 0 ,b ] .52. y = π x ² ²
Encontre ∫ 0 5 f x d x se f x = 3 ,     p a r a   x3 x ,     p a r a   x ≥ 3
Suponha que f tenha uma valor mínimo absoluto m e um valor máximo absoluto M . Entre quais dois valores ∫ 0 2 f x d x deve ficar? Que propriedade das integrais lhe permitem tirar esta conclusão?