Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução e Definição de Integral

Ver Teoria
Exercício 11123456789101213141516171819202122232425262728293031323334353637383940

Enunciado

ME02) O valor de ∫ - 1 1 x 3 + x 2018 sin 3 ⁡ x   d x é

  1. 3 2
  2. 1 2
  3. - 3 2
  4. - 1 2
  5. 0

Passo 1

Eita, que integral complicada de resolver. E agora? Olha só, fica tranquilo que você não vai precisar resolver mesmo essa integral. Porque? Veja bem, vamos supor que ao invés de:

f x = x 3 + x 2018 sin 3 ⁡ x

Tenhamos dentro da integral:

f x = x

Logo a integral daria:

∫ - 1 1 x   d x = x 2 2 x = - 1 x = 1 = 1 2 2 - - 1 2 2 = 1 2 - 1 2 = 0

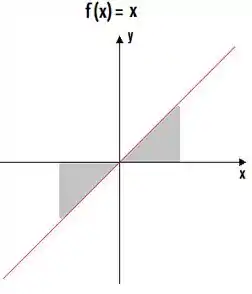
Eta, deu 0 ? Sim! Se fizemos a integral de uma função ímpar com limites de integração simétrica, vai ser como somar uma área pela sua negativa, então vai zerar. Uma boa primeira coisa pra tentar fazer então é ver se:

f x = x 3 + x 2018 sin 3 ⁡ x

É ímpar.

Passo 2

Pra uma função ser ímpar, tem que ser válido:

f x = - f - x

Pra achar f - x , fazemos:

f - x = - x 3 + - x 2018 sin 3 ⁡ - x

Como:

- x 3 = - 1 x 3 = - 1 3 ∙ x 3 = - x 3

sin ⁡ x = - sin ⁡ - x →   sin 3 ⁡ x = - sin 3 ⁡ - x →   sin 3 ⁡ - x = - sin 3 ⁡ x

- x 2018 = x 2018

Reescrevemos a função para:

f - x = - x 3 - x 2018 sin 3 ⁡ x

E fazendo - f - x , ficamos com:

- f - x = x 3 + x 2018 sin 3 ⁡ x

Veja que, de fato:

f x = - f - x

x 3 + x 2018 sin 3 ⁡ x = x 3 + x 2018 sin 3 ⁡ x

Ufa, nossa função é ímpar! A integral vai dar então 0 ! A resposta certa vai ser a Letra E

Resposta

L e t r a   E

Exercícios de Livros Relacionados

Encontre ∫ 0 5 f x d x se f x = 3 p a r ax3 xp a r ax ≥ 3
7. Calculea ) int_0^((pi)/(8)) cos^2 x d x
Nos Exercícios 51-54, use uma integral definida para determinar a área da região entre a curva dada e o eixo x no intervalo [ 0 ,b ] .52. y = π x ² ²
Encontre ∫ 0 5 f x d x se f x = 3 ,     p a r a   x3 x ,     p a r a   x ≥ 3
Suponha que f tenha uma valor mínimo absoluto m e um valor máximo absoluto M . Entre quais dois valores ∫ 0 2 f x d x deve ficar? Que propriedade das integrais lhe permitem tirar esta conclusão?