Lista de exercícios 10 – UFABC – Técnicas de integração– questão 22 item b
Encontre o comprimento do arco do gráfico da equação dada entre os ponto P e Q ou no intervalo especificado.
b)
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
Talvez você tenha medo de mexer com funções hiperbólicas, mas fique tranquilo, eu também tenho e estamos juntos nessa.
Mas saiba que as propriedades delas são parecidas com as funções trigonométricas que já conhecemos.
Bom, pede-se o comprimento de um arco, ou seja, o comprimento da linha de uma função de um ponto até o outro.
E o comprimento do arco que queremos saber é esse:
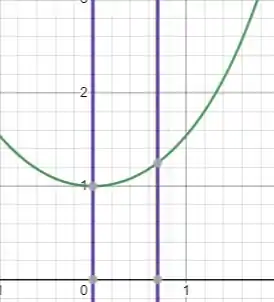
De um ponto na linha verde até o outro.
Duas coisas precisamos ter em mente quando queremos calcular o comprimento de um arco: saber derivar e a seguinte formula na qual aplicamos essa integração:
Onde é a função, “a” e “b” os limites de integração
Bom, já tendo a faca e o queijo na mão, vamos lá?
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Temos então a nossa função
Aplicando então na fórmula:
Bom, paras as funções hiperbólicas temos que . Assim temos que a nossa função fica:
Pois:
Passo 3
Lembra que falei que algumas das propriedades das funções hiperbólicas são parecidas com as trigonométricas? Então a integral do cosseno hiperbólico é o seno hiperbólico.
Fica mais fácil se passarmos o seno hiperbólico pro seu numeral, que é:
Assim então:
Então:
Resumindo:
O comprimento do arco vale 0,75 unidades. Sacou, carinha