Considere o seguinte gráfico da função
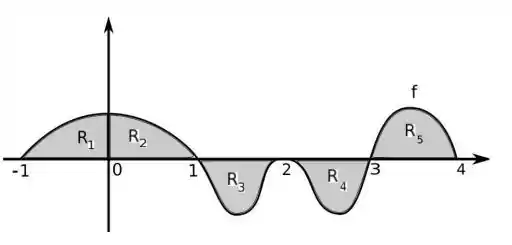
Sabendo que as áreas das regiões , , , e são:
.
Calcule:
Passo 1
Bom, vamos lá! O problema quer que a gente calcule várias integrais, mas ainda não sabemos calcular isso. Agora, o que o problema deu pra gente foram as áreas das regiões do gráfico!
Então uma coisa que a gente precisa saber que que a integral de uma função representa a área abaixo da curva dessa função! Como ele deu as área pra gente, aí podemos calcular as integrais.
Na primeira integral temos
Isso vai ser a área de à . Sabemos que a área dessa região é , logo a integral vai ser:
Passo 2
A integral seguinte, temos:
Usando a mesma lógica, vamos ver que a integral vai ser a soma das áreas das regiões e .
Agora, precisamos observar uma coisa muito importante, aqui, temos uma parte da função acima do eixo e outra abaixo.
Apesar de não existir área negativa, existe integral negativa. Portanto, temos que levar em consideração que a área de vai fazer uma contribuição negativa por estar abaixo do eixo x. A integral então vai ser:
Passo 3
Por último temos:
Como a gente já calculou , podemos separar como:
Que dá no mesmo que somar todas as áreas, como você preferir... mas temos que lembrar que a área de também está abaixo do eixo x. Então ficamos com:
Substituindo temos: