Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução e Definição de Integral

Ver Teoria
Exercício 32123456789101112131415161718192021222324252627282930313334353637383940

Enunciado

UnB – Cálculo I – Lista16 – 1g

Calcule a integral.

∫ x x 2 + x + 1 d x

Passo 1

Para facilitar nosso cálculo, a gente faz essa transformação:

x 2 + x + 1 = x 2 + x + 1 4 + 3 4 = x + 1 2 2 + 3 2 2

Assim, a gente esboça a seguinte figura:

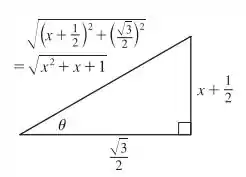
Passo 2

A gente tem que x + 1 2 = 3 2 tg ⁡ θ . Assim, se fizermos a derivada de x , a gente tem d x = 3 2 sec 2 ⁡ θ d θ e temos x 2 + x + 1 = 3 2 sec ⁡ θ .

Passo 3

Assim, o valor da nossa integral é:

∫ x x 2 + x + 1 d x = ∫ 3 2 tg ⁡ θ - 1 2 3 2 sec ⁡ θ 3 2 sec 2 ⁡ θ d θ = ∫ 3 2 tg ⁡ θ - 1 2 sec ⁡ θ d θ =

∫ 3 2 tg ⁡ θ sec ⁡ θ d θ - ∫ 1 2 sec ⁡ θ d θ = 3 2 sec ⁡ θ - 1 2 ln ⁡ sec ⁡ θ + tg ⁡ θ + C 1 =

x 2 + x + 1 - 1 2 ln ⁡ 2 3 x 2 + x + 1 + 2 3 x + 1 2 + C 1 =  

x 2 + x + 1 - 1 2 ln ⁡ 2 3 x 2 + x + 1 + x + 1 2 + C 1 =

x 2 + x + 1 - 1 2 ln ⁡ 2 3 - 1 2 ln ⁡ x 2 + x + 1 + x + 1 2 + C 1 =

x 2 + x + 1 - 1 2 ln ⁡ x 2 + x + 1 + x + 1 2 + C

Onde C = C 1 - 1 2 ln ⁡ 2 3 .

Resposta

x 2 + x + 1 - 1 2 ln ⁡ x 2 + x + 1 + x + 1 2 + C .

Exercícios de Livros Relacionados

Encontre ∫ 0 5 f x d x se f x = 3 p a r ax3 xp a r ax ≥ 3
7. Calculea ) int_0^((pi)/(8)) cos^2 x d x
Nos Exercícios 51-54, use uma integral definida para determinar a área da região entre a curva dada e o eixo x no intervalo [ 0 ,b ] .52. y = π x ² ²
Encontre ∫ 0 5 f x d x se f x = 3 ,     p a r a   x3 x ,     p a r a   x ≥ 3
Suponha que f tenha uma valor mínimo absoluto m e um valor máximo absoluto M . Entre quais dois valores ∫ 0 2 f x d x deve ficar? Que propriedade das integrais lhe permitem tirar esta conclusão?