Considere a equação diferencial

a) Mostre que é ponto singular desta equação diferencial

b)Determine a relação de recorrência, a equação indicial e suas raízes

c)Determine a solução em série de Frobenius em torno de , correspondente a maior raiz da equação indicial. Determine a expressão do termo geral desta solução.

d)Qual é o raio mínimo de convergência da série de potências da solução em c) ?

b) Determine a relação de recorrência, a equação indicial e suas raízes

Para fazer isso, vamos ter que utilizar aquela solução proposta pelo Frobenius(Que na realidade é uma aplicação da equação de Euler-Cauchy na teoria de séries!)

Derivando duas vezes:

OBS: Repara que a gente não aumenta o número inicial do somatório para essa série!! Ela começa em 0!! O motivo disso é porque nas outras séries de potência o menor termo é uma constante, nessa série o menor termo tem potência de , logo ele não se anula quando derivamos!

Substituindo isso na EDO:

Ajeitando os somatórios:

Bem, quase todos os somatórios tem como expoente e todos tem o somatório começando em , o que temos que fazer aqui é ajeitar o único que está diferente:

Bem, a gente começa ajeitando para ficar no mesmo índice! Então é só tomar , substituindo isso no somatório o índice da potência vai ficar certo:

Mas calma, agora o somatório começa em , os outros começam em ! Não tem jeito, vamos ter que arrumar os outros somatório forçando eles a começar em , isso é só abrir abrir o somatório galera, vamos lá:

Vamos ver o outro somatório

Ok, temos os 3 somatórios começando na mesma potência e iniciando no mesmo índice! Tudo certo! Vamos voltar então a equação, é só substituir esses 3 somatórios que calculamos agora:

Vamos juntar tudo o que temos na mesma potência:

Show de bola, agora nota o seguinte. Já que a equação abaixo precisa satisfazer a igualdade:

Ou seja, precisa ser igual a zero para todos os (inclusive os diferentes de zero), a única maneira disso ser verdade é se os coeficientes forem zero, ou seja:

E isso simultaneamente! Veja que, as raízes dos polinômios de no interior das duas primeiras equações são:

E:

Portanto, pra que as três equações sejam iguais a zero, a escolha de um dos coeficientes deve ser zero!

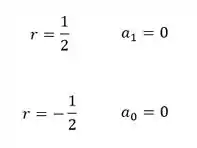
Como o enunciado pede pra gente se preocupar com a maior raiz somente, a equação indicial que queremos é:

No nosso caso então, a solução terá a seguinte cara:

Vamos para a relação de recorrência, que se obtém só igualando o coeficiente da série a :

Rearrumando:

Não esquece que a somatório começa em hen! Por isso é para , agora substituindo :

Como nesse caso, o termo e todos os coeficientes que dependerem dele, serão zero, então todos os coeficientes impares zeram. Vamos então substitui por para que possa correr todos os números ao invés de só os pares . Nossa relação fica:

Aplicando a recorrência:

Etc... Achamos então a relação:

E nossa solução é:

E só pra ficar bonitinho, vamos voltar pra letra :

Se quiser você pode colocar em evidência como fizemos na teoria, e tratar ele como , porque é só uma constante e de qualquer forma a solução geral é dada pela combinação linear dessa com outra solução linearmente independente, e essa combinação linear implicaria em ter constantes multiplicando e , que seriam determinadas pelas condições iniciais ou de contorno.

E tcharã! Ufa! A expressão do termo geral dessa solução seria a que a gente colocou agora em cima, mas perceba que essa não é a solução geral! E nem temos a solução geral, porque a gente precisaria de outra solução linearmente independente dessa, e não temos! Isso por causa da diferença entre e ! Implicou que só saberíamos uma solução por esse método.

d)Qual é o raio mínimo de convergência da série de potências da solução em c) ?

Hmmm, então ele quer saber o raio de convergente dessa série, isso é ponto singular, não ordinário, então não sabemos o raio mínimo de convergência da série como era no ordinário, vamos ver a cara da série:

Partiu fazer um teste da razão e ver para que intervalo ele da menor que :

Deu pra cortar muita coisa já, vamos ajeitar isso daí:

Da pra cortar os fatoriais também, pois

Assim fica:

Sabemos que da pois , daí a gente conclui que ela é menor que 1 para todo , então o raio de convergência é infinito: