PUCRIO – Física 2 – 2020.1 – G3 – Discursiva
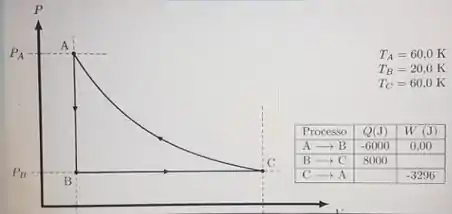
. Um gás ideal de é submetido ao seguinte ciclo representado no gráfico. Os processos são
: Isovolumétrico
: Isobárico
: Compressão Isotérmica
Utilizando as informações na tabela e no gráfico, encontre o valor do produto entre o número de mol desse gás e a constante dos gases ideias :
Passo 1
Vem comigo que a gente domina essa questão!
O enunciado pede o valor do produto . Podemos encontrá-lo analisando o processo isovolumétrico, já que sabemos o valor do calor e do trabalho nesse processo e com isso a primeira lei da termodinâmica fica da seguinte maneira:
O gás ideal de é uma molécula poliatômica e assim a energia interna é dada por:
E a variação é:
Se isolarmos o produto , temos:
Então podemos calcular esse produto, já que sabemos o valor de nesse processo e sabemos a temperatura em e .
Mãos à obra então!
Passo 2
Temos que:
S8ubstituindo com o que sabemos, temos:
Então temos que:
Prontinho, chegamos no que o enunciado queria!