Ciclos Termodinâmicos e Máquinas Térmicas
Certa quantidade de gás ideal, sendo , descreve o ciclo mostrado na figura ao lado. Os processos e são adiabáticos e os processos e são isobáricos. Dados e
Obs.: (reproduza as tabelas no caderno de respostas).
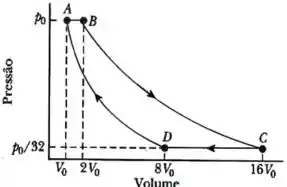
- Determine os valores de temperaturas nos pontos A, B, C e D.
- Determine os valores de .
- Determine o trabalho realizado, o calor recebido e a variação da energia interna do gás, para cada processo e preencha a tabela.
- O ciclo considerado descreve uma máquina térmica ou um refrigerador? Justifique.
- Calcule a eficiência (se for máquina), ou coeficiente de desempenho (se forrefrigerador).
Passo 1
a):
Primeiro vamos determinar apenas usando a equação dos gases:
Pra achar a temperatura de , basta a gente aplica o Piviti-Povóto:
Vamos usar Piviti-Povóto pra achar e :
E:
Passo 2
b):
Pra achar , a gente pode usar uma das transformações adiabáticas:
Só que, como:
Então:
Passo 3
c):
Vamos começar por
O processo é uma transformação adiabática. Logo:
Então, vamos calcular a variação de energia interna:
Então:
Processo :
É um processo isobárico. Então é muito fácil calcular o trabalho, porque ele é dado por:
Além disso, o calor pode ser calculado por:
E então:
Processo
Outro processo adiabático, então:
Então, vamos fazer como na outra:
Então:
Processo
Finalmente, o processo , outro processo isobárico. Então:
Além disso:
Então:
Ufa! Acabamos. Vamos completar a tabela então:
Passo 4
d):
Pra saber isso, basta a gente calcular o trabalho total, a soma de todos os trabalhos. Se ele for positivo, é uma máquina térmica, se for negativo, é um refrigerador.
Como o trabalho é maior que zero, isso é uma máquina térmica.
Passo 5
e):
O rendimento é calculado por:
Mas quem é o calor
É o calor despejado no sistema pela fonte quente. Como sabemos quem ele é? Bom, como é calor entrando no sistema, ele tem que ser positivo.
Então dê uma olhada na tabela.
Pela tabela, esse é o calor:
Então:
Resposta
a):
b):
c):
d):
Máquina Térmica.
e):