Origem do Exercício
Considere o ciclo mostrado na figura abaixo em que um gás ideal passa pelos estados . Em quais etapas o gás cede calor, isto é, ?
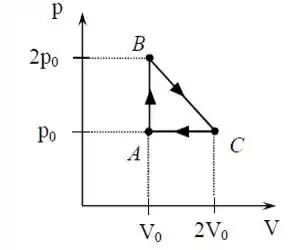
Passo 1
No processo , não há variação da temperatura. Veja só:
Em
Em
Assim, como não há variação de temperatura, não há variação de energia interna:
Isso leva à:
Como o gás se expandiu, temos que , logo
Passo 2
No processo , o volume é constante, assim, o trabalho é nulo e teremos:
Como a variação da energia interna é dada por:
Como é dada por:
E é dada por:
Assim:
E então,
Passo 3
No processo , temos que a variação de energia interna é dada por
Olhando o diagrama
E
Assim
Como a pressão nesse processo é constante o trabalho é dado por
Assim a primeira lei fica
Resposta
f)
Exercícios de Livros Relacionados
Quando um sistema é levado do estadoipara o estadofao longo da trajetória i a f na figura, Q=50c a l e W=20c a l . Ao longo da trajetória i b f , Q=36c a l . (a) Qual o valor de W ao longo da trajetór
Uma amostra de gás sofre uma transição de um estado inicial a para um estado final b por três diferentes trajetórias (processos), como mostra o diagrama p - V da figura, onde V b = 5,00 V i . A energi
Estime o rendimento máximo de um motor de automóvel que tenha uma razão de compressão de 8 : 1 . Suponha que a máquina opere no ciclo Otto, e que γ = 1.4 .
Uma amostra de 1 mol de gás N 2 , a 20°C e 5 atm, expande-se adiabaticamente até que sua pressão seja igual a 1 atm. Ele é, então, aquecido à pressão constante até que sua temperatura seja novamente 2
Um gás ideal, a uma temperatura inicial T 1 e com um volume inicial de 2,0m 3 , sofre uma expansão adiabática para um volume de 4,0m 3 , depois uma expansão isotérmica para um volume de 10m 3 e, final