A figura abaixo mostra o ciclo a que é submetido de um gás ideal. As temperaturas são , e .
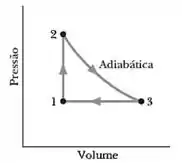
- Calcule e .
- Obtenha o coeficiente adiabático e diga se o gás é monoatômico, diatômico ou poliatômico.
- Determine, justificando, o calor trocado, , o trabalho realizado, , e a variação de energia interna, , para cada um dos processos, , , e para o ciclo. Preencha a tabela abaixo
- Calcule a eficiência da máquina que trabalha conforme esse ciclo.
Dados:
Passo 1
Estamos falando de um mol de um gás ideal que obedece
Primeiro vamos obter as relações mais fáceis. O processo é uma transformação isovolumétrica
Já o processo é uma transformação isobárica (pressão constante)
Passo 2
Agora temos que procurar as razões pedidas pelo enunciado
A primeira delas é
Do processo temos que
Por outro, lado do processo
Substituindo temos
A segunda razão pedida é
Do processo temos que
Por outro lado, do processo
Substituindo
Passo 3
Em uma transformação adiabática o termo
é constante. Assim
Só que essas razões entre essas pressões e volumes já calculamos ;)
E esse é o valor de correspondente ao gás monoatômico.
Passo 4
Como o gás é monoâtomico a sua energia interna é dada por (lembrando que )
Vamos olhar cada um dos processos
No primeiro processo , temos uma transformação isovolumétrica, logo nesse caso o trabalho será nulo
A variação de energia interna é dada por
Agora usando a primeira lei para gases ideais, temos
Passo 5
No processo , temos uma transformação adiabática, onde não há troca de calor, ou seja,
Já a variação de energia interna é dada por
E agora usando a primeira lei para gases ideais, temos
Passo 6
E agora no processo , temos uma transformação isobárica. Nesse caso fica superfácil calcular o trabalho, já que a pressão é constante
Lembrando que
Já a variação de energia interna é dada por
Já o calor podemos obter usando a primeira lei para gases ideais
Passo 7
Agora vamos para o ciclo! No ciclo sabemos que a variação de energia interna é nula!
Já o trabalho no ciclo é a soma do trabalho em cada etapa
E o calor no ciclo podemos calcular usando a primeira lei
Ou você poderia ter somado os calores de cada um dos processos.
Passo 8
A eficiência da máquina que trabalha com esse ciclo é dada por
Onde é o calor fornecido ao gás, ou a energia da fonte quente. Como o calor que entra é somente , temos
Resposta
(a) e
(b) . Gás monoatômico
(c)
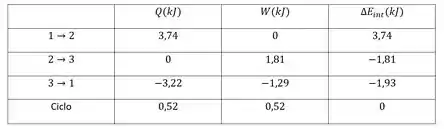
(d)