Uma certa quantidade de um gás ideal monoatômico é submetida ao seguinte ciclo, ilustrado na figura:
• : Uma expansão livre adiabática (ELA).
• : Uma redução isobárica de volume (IB).
• : Um aumento isocórico de pressão (IV).
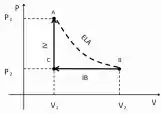
Com relação à energia interna U em cada estado e ao calor total QT trocado no ciclo podemos afirmar que:
(a) .
(b) .
(c) .
(d) .
Passo 1
Então, vamos analisar caso a caso aqui, com calma, ok?
temos uma expansão livre adiabática de um gás.
Por ser uma expansão livre, nós temos que .
Por ser adiabática, temos que .
Bom, se: , a gente chega à conclusão que: !
Com isso, se não variou a energia interna, !
Já temos um forte candidato à resposta, que é a letra (d).
Passo 2
temos uma redução isobárica de volume.
Com isso,
Como , o trabalho nesse processo é negativo!! Pois se trata de uma redução de volume, ok? Guarde isso.
Passo 3
Beleza, temos um aumento isocórico de pressão.
Então, , pois o volume não variou!!
E:
Passo 4
Cara, além disso tudo, nós temos que:
Então:
Mas repare que nós só tivemos trabalho em e esse trabalho foi negativo! Dessa forma, , também!!
A alternativa que diz que e é a letra (d)!!
Resposta
Alternativa (d).