Um mol de um gás ideal ocupa um volume sob uma pressão . A partir desse estado, ele é submetido aos seguintes processos reversíveis: um aquecimento isovolumétrico até a sua pressão quintuplicar; depois () uma expansão isotérmica até a pressão original e, finalmente, uma transformação isobárica voltando ao estado inicial. Sabe-se que para esse gás a capacidade térmica molar a volume constante é onde é a constante universal dos gases ideais.
- Desenhe o ciclo do gás no diagrama , indicando os valores de e nos estados 1, 2 e 3.
- Identifique em quais etapas o gás RECEBE calor e determine o valor total do calor recebido pelo gás.
- Identifique em quais etapas o gás CEDE calor e determine o valor total do calor cedido pelo gás.
- Determine o trabalho total realizado pelo gás durante um ciclo.
- Esse gás é monoatômico ou diatômico? Justifique!
Passo 1
a) O desenho vai facilitar bastante a nossa visualização do processo, então vamos lá!
Primeiramente vamos anotar cada trecho do ciclo, para depois projetarmos no gráfico:
Um aquecimento isovolumétrico até a sua pressão quintuplicar.
,
como , temos:
() Uma expansão isotérmica até a pressão original.
Uma transformação isobárica voltando ao estado inicial.
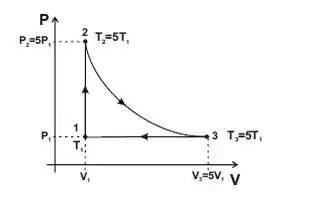
Passo 2
b) Vamos utilizar o próprio gráfico que nós construímos para responder está questão. Nele é possível a gente observar que a única etapa em que o gás cede calor ao ambiente é na etapa , onde a temperatura do gás diminui. Portanto, vamos calcular a quantidade de calor que é recebida pelo gás nas etapas e :
Vamos agora somar o calor recebido total nesses dois trechos:
Passo 3
c) Bom, nos restou agora calcular a quantidade de calor que o gás cede para o ambiente e, como já observamos no gráfico, esse calor corresponde ao trecho .
Passo 4
d) Galera, nós sabemos que a variação da Energia interna é uma função de estado. Certo? Isso quer dizer que que depende só do estado final e inicial do processo. Logo, podemos afirmar que Portanto:
Passo 5
e) Pelo teorema da equipartição da energia, cada grau de liberdade no movimento do átomo acrescenta ao valor de . Para um gás monoatômico temos três graus de liberdade, Portanto o gás com é diatômico. Para um gás diatômico temos de três a sete graus de liberdade, mas devido a efeitos quânticos nem todos estão disponíveis. As temperaturas “usuais” temos três graus de translação e dois de rotação, totalizando cinco graus de liberdade ativos: .
Resposta
a)
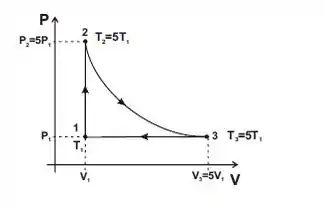
b) e ;
c) ;
d)
e) é diatômico.