Um mol de um gás monoatômico ideal realiza o ciclo mostrado na figura. O processo é uma contração isotérmica reversível. São conhecidos e e sabe-se que e . Suponha conhecidas as relações entre , , e o número de graus de liberdade do gás. Calcule, com justificativas, em função apenas de e :(Observação: Não é necessário calcular valores numéricos para logaritmos.)

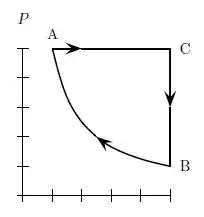
1. O trabalho líquido feito sobre o gás no ciclo, deduzindo as expressões utilizadas.
2. O calor transferido em cada etapa, deixando claro se este foi absorvido pelo gás ou cedido por ele.
3. O rendimento do ciclo.

b):

Vamos lá:

O processo é isotérmico, logo:

E:

Ué, mas por que eu coloquei um sinal negativo ali? Bem, é que agora estamos analisando o calor recebido pelo gás, então, o trabalho que aparece ali encima é o trabalho realizado pelo gás, que é igual ao trabalho realizado sobre o gás vezes

E como é negativo, esse calor foi rejeitado pelo gás pro ambiente.

Esse calor é trocado à pressão constante, então vamos usar:

Vamos usar o piviti-povóto pra escrever em função de

Então:

E como:

Então:

Já que

Como é positivo, o calor é absorvido pelo gás.

Usando, pra um gás monoatômica:

Então:

Nesse caso, o volume é constante, então usamos

Vamos usar Piviti-Povoto pra achar a relação entre e

Como

Então:

Usando:

Então:

Usando de novo aquela parada:

Então:

E como é negativo, é calor perdido pelo gás.

c):

O rendimento é calculado assim galera:

A gente já calculo o trabalho do ciclo, certo?

O calor é o calor quente, ou seja, o calor fornecido pela fonte quente. Isso é, o calor que entra no sistema, logo:

E:

Então: