Uma máquina térmica opera segundo o ciclo conforme figura abaixo.

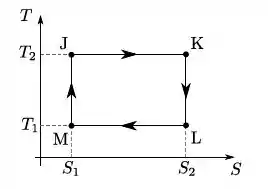
Assinale a ÚNICA alternativa correta:

(a) Qualquer outra máquina que opere entre não poderá ter rendimento maior que o desta.

(b) O rendimento dessa máquina é dado por

(c) O processo JK corresponde a uma compressão isotérmica.

(d) O trabalho realizado por essa máquina em um ciclo é .

Antes de analisar as alternativas, vamos lembrar da primeira lei da termodinâmica. Essa lei nos diz que:

I – Verdadeira. A máquina representada na figura se refere a uma máquina térmica de Carnot! E nenhuma máquina existente possui eficiência maior do que a máquina de Carnot.

II – Falsa. O rendimento de uma máquina de Carnot é dado por , só que a temperatura do reservatório quente nesse caso é (que é a maior) e do reservatório frio é (que é a menor). Logo, o rendimento seria (o que a frase afirma troca por na conta, então tá errado).

III - Falsa. De fato esse é um processo isotérmico, mas é um processo onde o gás GANHA calor (por que a variação de entropia é positiva). Se a gente lembrar do ciclo de Carnot no diagrama esse processo corresponde a uma expansão isotérmica!

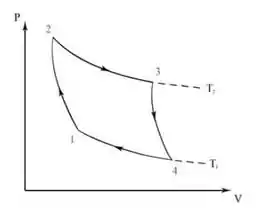
IV – Falsa. Atente que a figura acima se refere a um diagrama , então:

No ciclo temos que , logo

E o trabalho do ciclo nesse diagrama é a área do ciclo que é dada por