Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Primeira Lei da Termodinâmica em Ciclos

Ver Teoria
Exercício 5012345678910111213141516171819202122232425262728293031323334353637383940414243444546474849515253545556575859606162

Enunciado

Questão 9, UFF, P1-2016.1

Um gás ideal monoatômico sofre uma expansão isotérmica do ponto A para o ponto B, segundo o diagrama p V abaixo. Depois, ele é resfriado a volume constante até o ponto C . A seguir, ele é comprimido isobaricamente até o ponto D e finalmente é aquecido e retorna ao ponto A isocoricamente.

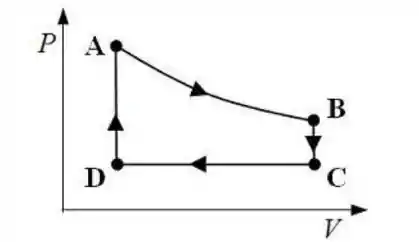
Dados: V A = V D =   2,00   L ; p A =   10,0   a t m ; P C =   2,00   a t m ; V B   =   V C =   4,00   L , T A =   327   ° C .

Qual é a Energia Térmica do gás no ponto B?

  1. 1,0 x 10 3 J
  2. 2,0 x 10 3 J
  3. 3,0 x 10 3 J
  4. 4,0 x 10 3 J
  5. 5,0 x 10 3 J

Dado:

R = 8,31 J / m o l . K

1 a t m = 10 5 P a

1 l = 10 - 3 m 3

Passo 1

Bom, a transformação do ponto A ao B é isotérmica. Logo, os pontos tem a mesma temperatura e, por consequência, a mesma energia térmica.

A energia térmica é dada por:

U = 3 2 n R T

Para um gás monoatômico. O valor da temperatura ( igual a temperatura de A ) e o valor de R já foram dados. Basta a gente achar o valor n .

Passo 2

Para achar o valor de n , podemos aplicar a equação dos gases perfeitos no ponto A . Nesse ponto, temos os valores de temperatura, pressão e volume:

P A V A = n R T A → n = P A V A R T A

Por causa do valor de R , precisamos converter as unidades das medidas:

P A = 10,0 a t m = 10,0.10 5 P a

V A = 2,0.10 - 3 m 3

T A = 327 + 273 = 600 K

Assim:

n = 10,0.10 5 . 2,0.10 - 3 8,31.600 ≅ 0,4   m o l

Passo 3

Temos tudo agora pra achar a energia térmica de B :

U B = 3 2 n R T B

Como:

T B = T A = 600 K

Então:

U B = 3 2 . 0,4 . 8,31 . ( 600 ) ≅ 3,0.10 3 J

Resposta

c)

Exercícios de Livros Relacionados

Quando um sistema é levado do estadoipara o estadofao longo da trajetória i a f na figura, Q=50c a l e W=20c a l . Ao longo da trajetória i b f , Q=36c a l . (a) Qual o valor de W ao longo da trajetór
Uma amostra de gás sofre uma transição de um estado inicial a para um estado final b por três diferentes trajetórias (processos), como mostra o diagrama p - V da figura, onde V b = 5,00 V i . A energi
Estime o rendimento máximo de um motor de automóvel que tenha uma razão de compressão de 8 : 1 . Suponha que a máquina opere no ciclo Otto, e que γ = 1.4 .
Uma amostra de 1 mol de gás N 2 , a 20°C e 5 atm, expande-se adiabaticamente até que sua pressão seja igual a 1 atm. Ele é, então, aquecido à pressão constante até que sua temperatura seja novamente 2
Um gás ideal, a uma temperatura inicial T 1 e com um volume inicial de 2,0m 3 , sofre uma expansão adiabática para um volume de 4,0m 3 , depois uma expansão isotérmica para um volume de 10m 3 e, final