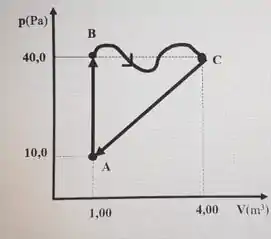
. Um determinado gás passa pelos processos termodinâmicos ilustrados no diagrama representado na figura abaixo. Inicialmente o gás no estado termodinâmico (a volume e pressão ), é submetido a um processo termodinâmico a volume constante. No estado termodinâmico (a volume e pressão ), novamente o gás é submetido a um processo termodinâmico de expansão. No estado (a volume e pressão ) o gás sofre processo termodinâmico linear de compressão até atingir novamente o estado . Sendo o trabalho total do gás no ciclo igual a , calcule o trabalho realizado no trecho à e determine a temperatura do gás no estado . Considere que o número de mols é tal que .
. e
. e
. e
. e
. e
. e
. Nenhuma das alternativas
. e
Passo 1
Vem comigo que a gente resolve esse problema!
Para achar o trabalho vamos usar o que sabemos do trabalho total, já que:
O trabalho já que o processo é a volume constante, então só ficamos com:
Então precisamos encontrar o trabalho e podemos fazer isso usando o fato de que o trabalho é igual a área da curva que indica o processo de nosso interesse.
Agora para achar o valor da temperatura no estado () vamos usar a equação dos gases ideias, dada por:
Assim temos que:
Vamos lá então!
Passo 2
Vamos primeiro encontrar o trabalho , ele é igual a área embaixo da reta . Olhando a figura vemos que essa região forma um trapézio, logo temos que:
Então:
Mas como o processo referente a esse trabalho é de compressão, esse trabalho é negativo, logo:
Passo 3
Agora que temos o trabalho podemos achar o , temos:
Então temos que:
Passo 4
Agora vamos achar a temperatura no estado , do passo temos que:
Do gráfico temos que , e segundo o enunciado . Com isso temos que:
Logo temos que:
Assim temos que a alternativa correta é a letra .
Resposta
. e