Quando um sistema passa do estado para o estado seguindo a trajetória como moastra a figura, e . Ao longo da trajetória , .
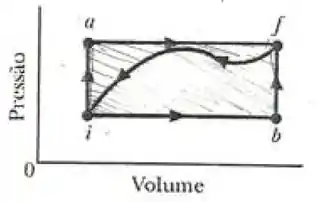
Encontre a variação de energia interna nas trajetórias e . Encontre também o trabalho aolongo da trajetória .
Considere a trajetória curva . Se o trabalho nessa trajetória é , encontre o calor
Considerando o ciclo , encontre o calor, o trabalho e a variação de energia interna do ciclo.
Passo 1
Quando temos um gráfico de pressão por volume, devemos imediatamente nos lembrar da Primeira Lei da Termodinâmica . Ahh...lembre-se que o trabalho será a área abaixo da curva e que a variação da energia interna não depende do caminho, e sim do ponto inicial e final! Agora vamos resolver essa questão!
Passo 2
Vamos primeiro achar a variação da energia interna nas trajetórias e . Como a gente lembrou no passo , a variação interna depende apenas do ponto incial e final, ou seja para as duas trajetórias, teremos a mesma variação da energia interna!
Para achar essa variação, como temos o calor e o trabalho , podemos achar a variação da energia interna, , usando a Primeira Lei da Termodinâmica! Se liga!
Substituindo, temos:
Ou seja:
Passo 3
Agora vamos achar o trabalho ao longo da trajetória . Como já sabemos o calor e já calculamos , podemos, com a Primeira Lei da Termodiâmica calcular o trabalho!
Passo 4
Agora, temos que trabalhar com a trajetória . Para determinar o calor , iremos utilizar novamente a Primeira Lei da Termodinâmica! Saca só...
Como ele nos dá o trabalho e nós já calculamos a variação interna para o ponto inicial e final, temos:
Ahh...se liga que a variação interna será , pois estamos indo de para .
Passo 5
Agora devemos considerar o ciclo . Como se trata de um ciclo, temo so ponto incial igual ao ponto final, desse modo, temos que a variação da energia interna é zero!
Agora que sabemos que a variação interna é zero, temos, pela Primeira Lei da Termodinâmica:
Podemos então calcular o calor, ou o trabalho! Vamos aqui calcular pelo trabalho. Como temos um ciclo, podemos deizer que:
Substituindo, temos:
Ou seja:
Resposta