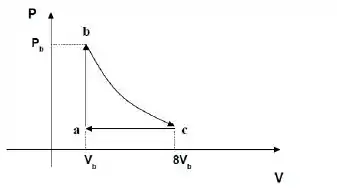
Um mol de gás ideal poliatômico percorre o ciclo reversível mostrado abaixo. O processo é uma expansão adiabática. Determine em termos da pressão e do volume :

1. A pressão e o volume em cada um dos pontos e do diagrama abaixo
2. O calor cedido pelo gás durante o processo e o calor absorvido pelo gás durante o processo
3. O trabalho realizado pelo gás no ciclo
4. A variacao da entropia em cada trecho e avariacao da entropia total
5. A eficiência do ciclo

1. Em um processo adiabático, a gente tem que

Ou seja, daqui podemos tirar que:

Mas quem é esse Ele é uma razão entre que para um gás ideal tem um valor fixo de , ou seja,

Portanto, podemos escrever olhando diretamente no gráfico que:

Pela igualdade que vimos no início para um processo adiabático, temos:

Com isso, temos que:

Por exame direto do diagrama, temos:

(b)

Para um gás ideal, temos

Com isto:

(c) Num ciclo a gente precisa lembrar que toda e qualquer propriedade em termodinâmica que seja função de estado, vai ter valor de zero. Isso acontece porque uma função de estado dependendo unicamente do seu estado inicial e final, não importa como você fez pra chegar até lá. Como (energia interna) é uma função de estado, num ciclo a gente parte de um ponto e retorna pra esse mesmo ponto ao final do processo, e portanto,

(d) Para um processo ADIABÁTICO, temos que , ou seja, não há perda ou ganha de calor no sistema, e, portanto, para um processo reversível, temos que:

Logo, para qualquer processo adiabático e reversível.

Para cada trecho precisamos calcular então:

Para um processo isocórico, que é mantido o volume constante, temos que pela primeira lei da termodinâmica:

porque temos que ele depende da variação de volume do meio.

Portanto:

Para um gás ideal podemos ter a relação:

Pelos dados já encontrado anteriormente nos itens acima, temos:

Considerando , temos:

Logo,

(e) A eficiência do ciclo é dada por definição como:

Ou seja, a eficiência é de 60,7%