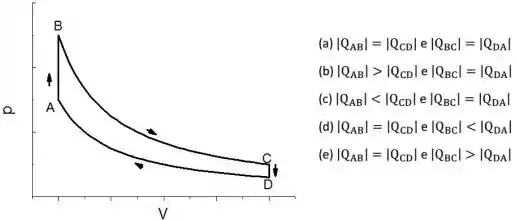
O ciclo mostrado no diagrama PV da figura é composto por dois trechos a volume constante e dois trechos a temperatura constante. Sobre os valores absolutos do calor trocado em cada trecho do ciclo pode-se dizer que:
Passo 1
Bem, em um processo isocórico (isovolumétrico), temos que o valor de é:
Além disso, como os processos e são isotérmicos ( e ), temos que . Ou seja, se em um, a temperatura aumenta, no outro, terá que diminuir para voltar ao valor inicial.
Como nosso problema está interessado nos módulos de , esse sinal não fará diferença!
Dessa forma: .
Já eliminamos a (b) e a (c)!
Passo 2
Agora vamos olhar essas isotérmicas aí. Vem comigo:
Sabemos que a variação de energia interna pode ser calculada por:
Como não estamos variando a temperatura, pela fórmula:
Vemos que nesses dois casos, ok?
E, pela primeira fórmula:
Passo 3
Beleza, lembrando que:
Isso quer dizer que seria a área embaixo das curvas, nesse diagrama!!
Olhando para o gráfico, vemos que a área embaixo de é maior que a área em .
Opa, se nesses dois processos, então, como estamos querendo os módulos de , vamos ficar com:
E a alternativa que junta isso tudo é a (e)! Resolvido!
Resposta
Alternativa (e).