Suponha que de um gás ideal monoatômico ( ) descreva um ciclo de Carnot que opera com entre as temperaturas de de (ver figura). A pressão em é . O volume é 2 vezes o volume .
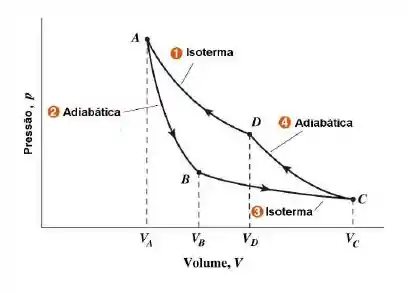
- Calcule o volume nos pontos do diagrama da figura.
- Determine o trabalho realizado, o calor recebido e a variação da energia interna do gás, para cada processo e preencha a tabela (reproduza a tabela no caderno de respostas).
- O ciclo considerado descreve uma máquina térmica ou um refrigerador? Justifique.
- Calcule a eficiência (se for máquina), ou coeficiente de desempenho (se for refrigerador).
- Obtenha a variação de entropia do gás em cada etapa do ciclo e represente o ciclo num diagrama (temperatura em função da entropia), identificando os estados .
Passo 1
O primeiro passo a se fazer quando a gente tem um exercício com bastante informações é organizá-las de acordo com o que estamos querendo obter. Neste exercício temos informações o suficiente para obtermos o então vamos calculá-lo pela equação de Clapeyron:
Como , temos que:
No processo adiabático, mostrado nos trechos e , vale a equação:
e
Logo:
Passo 2
O cálculo do Trabalho, quantidade de calor e variação da energia interna, é basicamente aplicação das formulas da Primeira Lei, onde:
As isotermas para cálculos do trabalho são dadas por:
Tá, mas e agora?
Agora, vamos calcular cada Q (J), W (J), ∆E (J) para cada trecho do ciclo.
Para o trecho :
, expansão adiabática;
Para o trecho
, processo isotérmico
Para o trecho :
, expansão adiabática;
Para o trecho :
, processo isotérmico
No ciclo, podemos afirmar que , pois a energia interna depende so de estado final e e inicial. Então conclui-se que .
Para nos organizarmos melhor, vamos fazer uma tabela, onde colocaremos os valores do trabalho, calor e variação da energia interna calculados acima:
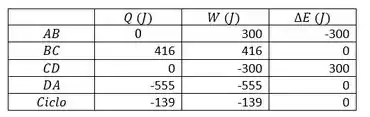
Passo 3
O ciclo esquematizado descreve um refrigerador, já que retira calor do reservatório frio () e cede calor ao reservatório quente ().
O coeficiente de desempenho pode ser calculado como:
Passo 4
Pessoal, tanto no trecho e , a variação da entropia é dada por:
, pois são trechos adiabáticos.
No trecho
Analogamente para o trecho :
Representando esquematicamente o exercício, temos:
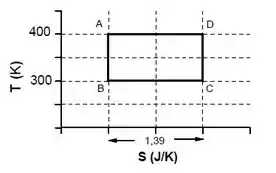
Resposta
Ei, a resposta está no passo a passo :)