Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Primeira Lei da Termodinâmica em Ciclos

Ver Teoria
Exercício 1812345678910111213141516171920212223242526272829303132333435363738394041424344454647484950515253545556575859606162

Enunciado

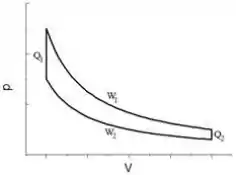
A figura mostra, no plano p   v s   V , uma máquina térmica baseada no ciclo de Stirling (duas isotermas e duas isocóricas). Nela estão assinalados Q 1   e   Q 2 , os valores absolutos do calor trocado em cada trecho a volume constante, e W 1 e W 2 , os valores absolutos do trabalho realizado pelo gás em cada trecho isotérmico. Assinale a expressão que representa a eficiência desta máquina térmica:

A) ( W 1 - W 2 ) / Q 1

B) ( W 1 - W 2 ) / ( Q 1 - Q 2 )

C) ( W 1 - W 2 ) / ( W 1 + Q 1 )

D) ( W 1 - W 2 ) / ( W 2 + Q 2 )

E) ( W 1 - W 2 ) / ( W 1 -   Q 1 )

Passo 1

Temos que o trabalho é dado por:

∫ P d V

Assim, o trabalho na expansão isotérmica é positivo, sendo negativo na compressão isotérmica. Nas isocóricas o trabalho é nulo. Portanto o trabalho realizado no ciclo será: W t o t a l = W 1 - W 2 .

Passo 2

Como nas isotermas U = 0 , temos que Q = W p e l o   g á s ( 1 a Lei). Portanto, o calor será positivo na expansão isotérmica e negativo na compressão. Quanto às isocóricas, como o trabalho é nulo, U =   Q ( 1 a Lei). Portanto, o calor será positivo no aquecimento isocórico e negativo no resfriamento. Assim, Q e n t r a = W 1 + Q 1 . Dessa forma, o rendimento será: η = ( W 1 - W 2 ) / ( W 1 + Q 1 )  

Resposta: letra (c).

Resposta

Alternativa (c).

Exercícios de Livros Relacionados

Quando um sistema é levado do estadoipara o estadofao longo da trajetória i a f na figura, Q=50c a l e W=20c a l . Ao longo da trajetória i b f , Q=36c a l . (a) Qual o valor de W ao longo da trajetór
Uma amostra de gás sofre uma transição de um estado inicial a para um estado final b por três diferentes trajetórias (processos), como mostra o diagrama p - V da figura, onde V b = 5,00 V i . A energi
Estime o rendimento máximo de um motor de automóvel que tenha uma razão de compressão de 8 : 1 . Suponha que a máquina opere no ciclo Otto, e que γ = 1.4 .
Uma amostra de 1 mol de gás N 2 , a 20°C e 5 atm, expande-se adiabaticamente até que sua pressão seja igual a 1 atm. Ele é, então, aquecido à pressão constante até que sua temperatura seja novamente 2
Um gás ideal, a uma temperatura inicial T 1 e com um volume inicial de 2,0m 3 , sofre uma expansão adiabática para um volume de 4,0m 3 , depois uma expansão isotérmica para um volume de 10m 3 e, final