Um sistema termodinâmico passa do estado para o estado , do estado para o estado e de volta para o estado , como mostra o diagrama da figura abaixo. A escala do eixo vertical é definida por , e a escala do eixo horizontal é definida por . Complete a tabela da figura abaixo introduzindo um sinal positivo, um sinal negativo ou um zero nas células indicadas. Qual é o trabalho líquido realizado pelo sistema em um ciclo ?
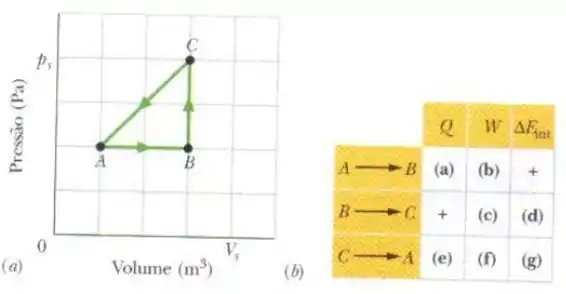
Passo 1
O problema nos pede para analisarmos os processos em separado e assim identificarmos o sinal de e
Para começar a estudar os processos, vamos primeiro descobrir a escala de cada eixo do gráfico, no eixo temos que então cada quadrado vale
E no eixo , então cada quadrado vale .
Agora vamos analisar o processo
Como é um processo em que há expansão (está aumentando), então
Pela primeira lei temos
Como
Então a soma de dois termos positivos dá necessariamente um termo positivo
Assim,
Vamos estudar agora o processo
Este processo é um processo a volume constante, então
Se trabalho é zero e o enunciado nos fornece que então pela primeira lei temos
Então
Agora, vamos estudar o processo
Como o volume diminui, temos que
Como temos um ciclo, temos que em a variação da energia interna é zero
Como a variação nos processos e são positivos, então para que a variação dê zero, então a variação de energia interna em tem que ser negativa
Agora para descobrir o sinal de , vamos analisar a primeira lei
Se e são negativas então é negativo
Então fica assim a tabela
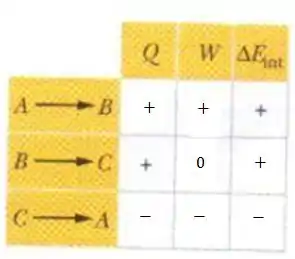
Passo 2
O módulo do trabalho de um ciclo é a área interna do ciclo, então basta a gente calcular a área interna do triângulo.
Como sabemos o valor de cada quadrado podemos substituir:
Como terminamos de dizer:
Como o processo envolve um trabalho negativo com módulo maior que o do trabalho positivo envolvido no processo , o trabalho do ciclo deve ser negativo.
Logo:
Resposta
a, b, c, d, e, f, g)
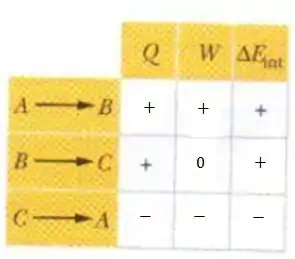
h)