Gases Ideais, Teoria Cinética dos Gases, Primeira Lei da Termodinâmica, Ciclos Termodinâmicos e Máquinas Térmicas
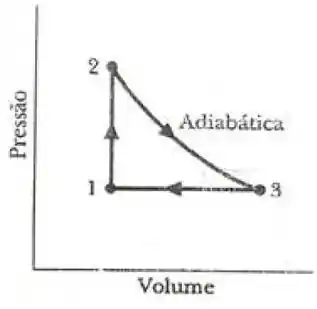
A figura mostra o diagrama co ciclo ao qual são submetidos de um gás ideal diatômico . As temperaturas nos pontos e são, respectivamente, , . Considere que a pressão no ponto é .
A massa molar do gás é .
Para o gás no estado correspondente ao ponto do diagrama, encontre a energia cinética média (translação e rotação) e a velocidade média quadrática das moléculas.
Determine o volume e a pressão no ponto . Encontre o volume e a temperatura no ponto . (Complete a tabela)
Determine a variação de energia interna, o calor e o trabalho para cada um dos processos representados na figura () e para o ciclo completo.
Passo 1
Quando falamos em gás ideal, devemos sempre lembrar da lei dos gases ideias:
E devemos prestar atençãoo se estamos tratando de uma gás monoatômico ou não!
Para determinar a energia cinética média, devemos lembrar da fórmula:
Como estamos considerando um gás diatômico, sabemos que a quantidade de graus de liberdade é .
Substituindo os valores, temos:
Passo 2
Vamos agora determinar a velocidade média quadrática :
substituindo os valores, temos:
Cuidado com as unidades, deve estar tudo no mesmo sistema de medidas, no caso, estamos usando o S.I! Por isso tivemos que multiplicar a massa molar!
Passo 3
Vamos primeiro reunir os dados que já temos:
Pelo diagrama, podemos tirar as seguintes conclusões:
Passo 4
Agora vamos calcular o volume no ponto e , que é o mesmo! Pela lei dos gases ideais, temos:
Substituindo os valores:
Passo 5
Vamos agora determinar a pressão no ponto . Pela lei dos gases ideais, temos:
Substituindo os valores:
Passo 6
Para determinar o volume no ponto , devemos lembrar da equação para o processo adiabático:
Para um gás diatômico, temos que . Substituindo, temos:
Passo 7
Para terminar o item , devemos utilizar a lei dos gases ideais para determinar a temperatura no ponto :
Substituindo os valores, temos:
Pronto, agora é só colocar os valores na tabela!
Passo 8
Para determinar a variação de energia interna, o calor e o trabalho, devemos nos lembrar da primeira lei da termodinâmica:
Para o processo , sabemos que o trabalho realizado é zero, pois a expansão é isovolumétrica.
Passo 9
Vamos agora determinar o calor, que será igual a variação de energia interna, se liga!
Para determinar , temos:
Onde é o calor específico molar a volume constante e, para o gás diatômico, é determinado por:
Substituindo na equação, temos:
Ahh..na equação acima, juntamos , o valor , não saiu da cartola!
Passo 10
Vamos agora analisar o processo ! Como processo é adiabático, temos que a variação do calor é zero:
Ou seja:
Vamos então determinar :
Lembrando que o gás é diatômico, por isso temos graus de liberdade!
Podemos ver pelo diagrama que o trabalho é de fato positivo!
Como temos uma redução na temperatura, sabemos que , portanto:
Passo 11
Vamos agora analisar o processo . Visto que é um processo isobárico, determinaremos primeiro o trabalho realizado:
Passo 12
Vamos agora determinar o calor, que para o gás diatômico, é:
Onde é o calor específico molar a pressão constante, e é dado por:
Como já calculamos , temos:
Substituindo na fórmula do calor, temos:
Passo 13
Para a energia interna, teremos:
Passo 14
Como era de se espera, termos para o ciclo:
Ou seja, devemos ter:
Calculando o calor total do ciclo:
Analogamente, teremos para o trabalho:
Show! Agora é só montar a tabela!
Resposta
